5. Bayesian Hierarchical Joint Modeling for Historical Data Borrowing

Authors

Daniel Sabanés Bové

Francois Mercier

Published

2026-08-20

The purpose of this document is to show a minimal workflow for Bayesian hierarchical joint modeling for historical data borrowing using the jmpost package.

Setup and load data

Here we execute the R code from the setup and data preparation chapter, see the full code here.

Descriptive analysis of the current study data

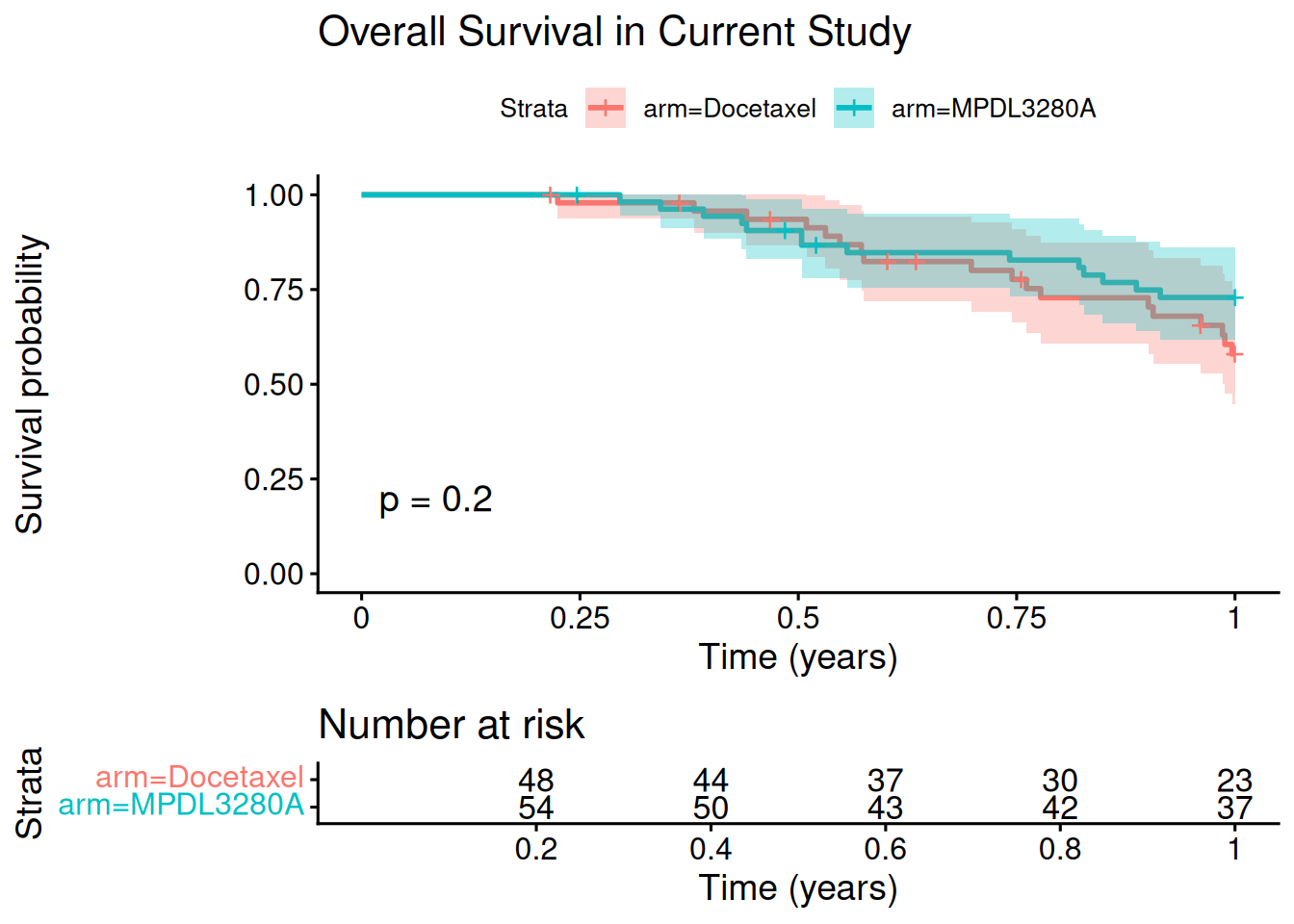
Let’s have a quick look at the (artificially reduced to maximum 1 year follow-up) current study data, in order to illustrate the typical situation where we have immature OS data:

Show the code

library(survival)


Attaching package: 'survival'

The following object is masked from 'package:brms':

    kidney

Show the code

library(survminer)

Loading required package: ggpubr


Attaching package: 'survminer'

The following object is masked from 'package:survival':

    myeloma

Show the code

# Overall Survival KM plot
fit_os_current <- survfit(Surv(os_time, os_event) ~ arm, data = current_os_data)

ggsurvplot(
    fit_os_current,
    data = current_os_data,
    risk.table = TRUE,
    pval = TRUE,
    conf.int = TRUE,
    xlab = "Time (years)",
    title = "Overall Survival in Current Study"
)

Ignoring unknown labels:
• colour : "Strata"

So no matter which model we might fit to this data, we will not be able to trust it to estimate the hazard ratio reliably.

Check compatibility of historical and current data

Just to mention that we would need to double check the compatibility of historical and current clinical trial design (including patient populations, endpoints, assessment schedules, etc.) and data distributions before applying any kind of historical data borrowing technique.

In our dummy example here, this is fulfilled by construction.

Fitting the joint model only to the historical data

The first step is to fit the joint model only to the historical data. In reality, this also includes model selection in order to determine:

choice of parametric baseline survival model (log-logistic, Weibull, etc.?)
selection of baseline covariates
choice of the TGI metric to correlate with the survival model, i.e. the link function (SLD, tumor growth rate, time to tumor regrowth, etc.?)

We have discussed model comparison and selection in session 3 here, so we will skip this step here and directly fit a joint model to the historical data only.

Show the code

historical_subj_df <- historical_os_data |>
    select(study, id, arm)
historical_subj_data <- DataSubject(
    data = historical_subj_df,
    subject = "id",
    arm = "arm",
    study = "study"
)

historical_long_df <- historical_tumor_data |>
    select(id, year, sld)
historical_long_data <- DataLongitudinal(
    data = historical_long_df,
    formula = sld ~ year
)

historical_surv_data <- DataSurvival(
    data = historical_os_data,
    formula = Surv(os_time, os_event) ~ ecog + age + race + sex
)

historical_joint_data <- DataJoint(
    subject = historical_subj_data,
    longitudinal = historical_long_data,
    survival = historical_surv_data
)

historical_joint_mod <- JointModel(
    longitudinal = LongitudinalSteinFojo(
        mu_bsld = prior_normal(log(65), 1),
        mu_ks = prior_normal(log(0.52), 1),
        mu_kg = prior_normal(log(1.04), 1),
        omega_bsld = prior_normal(0, 3) |> set_limits(0, Inf),
        omega_ks = prior_normal(0, 3) |> set_limits(0, Inf),
        omega_kg = prior_normal(0, 3) |> set_limits(0, Inf),
        sigma = prior_normal(0, 3) |> set_limits(0, Inf)
    ),
    survival = SurvivalWeibullPH(
        lambda = prior_gamma(0.7, 1),
        gamma = prior_gamma(1.5, 1),
        beta = prior_normal(0, 20)
    ),
    link = linkGrowth(
        prior = prior_normal(0, 20)
    )
)

options("jmpost.prior_shrinkage" = 0.999)

save_file <- here("session-bhm/histmod1.rds")
if (file.exists(save_file)) {
    historical_joint_results <- readRDS(save_file)
} else {
    historical_joint_results <- sampleStanModel(
        historical_joint_mod,
        data = historical_joint_data,
        iter_sampling = ITER,
        iter_warmup = WARMUP,
        chains = CHAINS,
        parallel_chains = CHAINS,
        thin = CHAINS,
        seed = BAYES.SEED,
        refresh = REFRESH
    )
    saveObject(historical_joint_results, file = save_file)
}

Let’s have a look at the results:

Show the code

vars <- c(
    "lm_sf_mu_bsld",
    "lm_sf_mu_ks",
    "lm_sf_mu_kg",
    "lm_sf_sigma",
    "lm_sf_omega_bsld",
    "lm_sf_omega_ks",
    "lm_sf_omega_kg",
    "beta_os_cov",
    "sm_weibull_ph_gamma",
    "sm_weibull_ph_lambda",
    "link_growth"
)

mcmc_historical_joint_results <- cmdstanr::as.CmdStanMCMC(historical_joint_results)

mcmc_historical_summary <- mcmc_historical_joint_results$summary(vars)

print(mcmc_historical_summary, n = 30)

# A tibble: 19 × 10
   variable           mean   median     sd    mad      q5     q95  rhat ess_bulk
   <chr>             <dbl>    <dbl>  <dbl>  <dbl>   <dbl>   <dbl> <dbl>    <dbl>
 1 lm_sf_mu_bsld…  3.77     3.77    0.0476 0.0465  3.69    3.85   1.02      399.
 2 lm_sf_mu_ks[1] -0.0763  -0.0487  0.283  0.259  -0.565   0.353  1.01      583.
 3 lm_sf_mu_ks[2] -1.15    -1.13    0.413  0.412  -1.83   -0.501  1.000     956.
 4 lm_sf_mu_kg[1] -0.592   -0.582   0.145  0.139  -0.860  -0.370  1.01      721.
 5 lm_sf_mu_kg[2] -0.863   -0.850   0.198  0.186  -1.22   -0.550  1.000     883.
 6 lm_sf_sigma     4.83     4.82    0.194  0.196   4.52    5.17   1.00      813.
 7 lm_sf_omega_b…  0.484    0.482   0.0383 0.0372  0.427   0.550  1.00      537.
 8 lm_sf_omega_k…  1.05     1.01    0.220  0.207   0.753   1.46   1.00      807.
 9 lm_sf_omega_k…  1.53     1.50    0.350  0.350   1.03    2.19   0.999     917.
10 lm_sf_omega_k…  0.495    0.486   0.110  0.105   0.333   0.693  1.00      846.
11 lm_sf_omega_k…  1.02     1.01    0.153  0.150   0.802   1.30   1.00      872.
12 beta_os_cov[1]  1.07     1.06    0.367  0.360   0.480   1.68   0.999     821.
13 beta_os_cov[2]  0.00793  0.00712 0.0158 0.0152 -0.0169  0.0354 0.998    1023.
14 beta_os_cov[3]  0.879    0.889   0.656  0.673  -0.227   1.95   1.00     1116.
15 beta_os_cov[4]  0.191    0.180   0.370  0.360  -0.413   0.812  1.00      947.
16 beta_os_cov[5]  0.302    0.308   0.356  0.381  -0.303   0.873  1.00      797.
17 sm_weibull_ph…  1.68     1.67    0.225  0.219   1.33    2.07   1.000     889.
18 sm_weibull_ph…  0.166    0.106   0.178  0.0983  0.0184  0.500  0.998    1014.
19 link_growth     0.862    0.843   0.370  0.362   0.286   1.48   1.00      876.
# ℹ 1 more variable: ess_tail <dbl>

Let’s also look at the covariate effect estimates again:

Show the code

os_cov_name_mapping <- function(surv_data) {
    surv_data_design <- as_stan_list(surv_data)$os_cov_design
    os_cov_names <- colnames(surv_data_design)
    old_coef_names <- as.character(glue::glue("beta_os_cov[{seq_along(os_cov_names)}]"))
    setNames(old_coef_names, os_cov_names)
}
os_cov_renaming <- os_cov_name_mapping(historical_surv_data)

draws_historical_joint_results <- mcmc_historical_joint_results$draws(vars)
draws_historical_joint_results <- do.call(
    rename_variables,
    c(list(draws_historical_joint_results), os_cov_renaming)
)
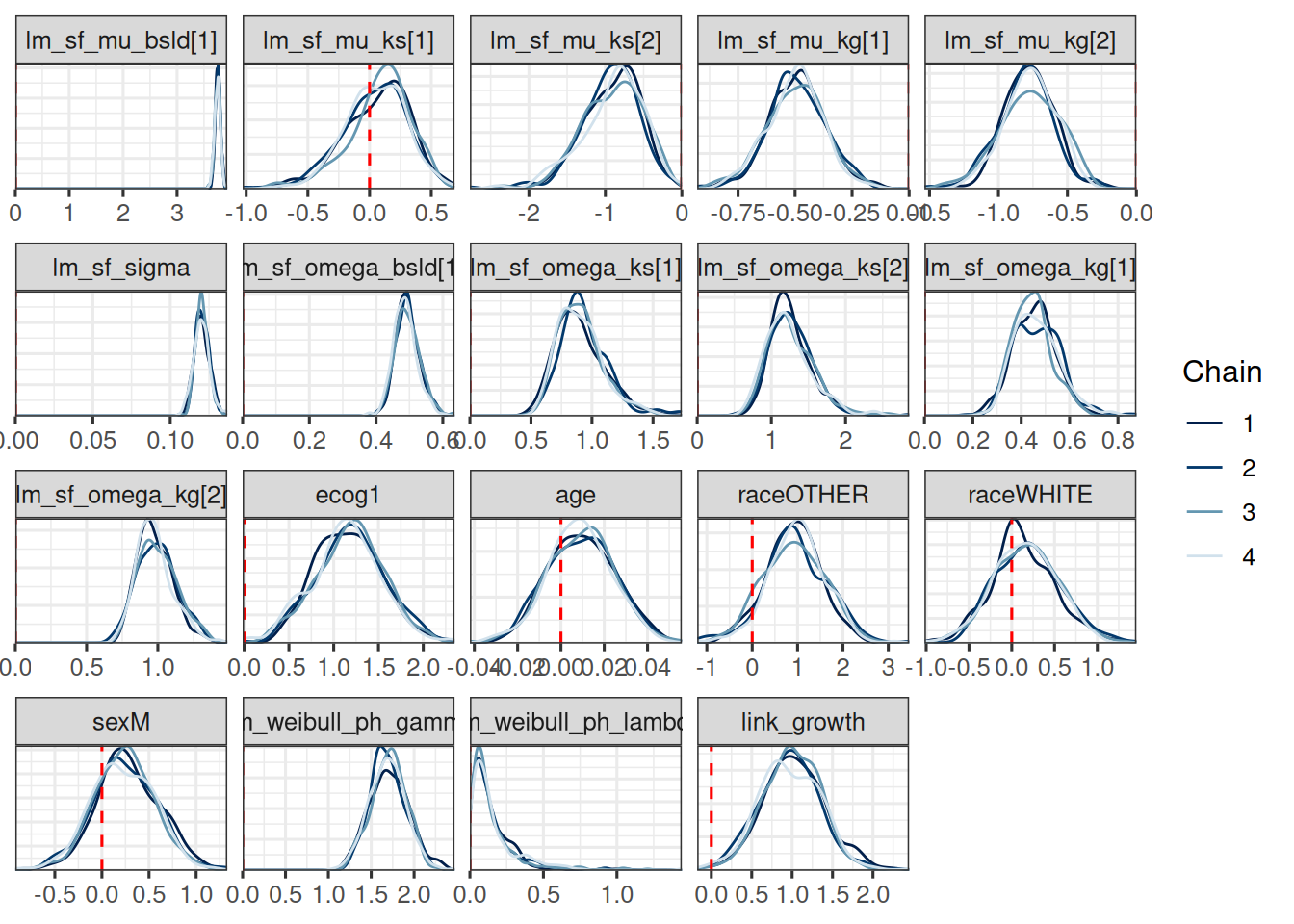
mcmc_dens_overlay(draws_historical_joint_results) +
    geom_vline(xintercept = 0, linetype = "dashed", color = "red")

Pool historical and current data

Now we pool the historical and the current data for the hierarchical joint modeling step:

Show the code

pooled_os_data <- bind_rows(
    historical_os_data,
    current_os_data
)
pooled_tumor_data <- bind_rows(
    historical_tumor_data,
    current_tumor_data
)
pooled_subj_df <- pooled_os_data |>
    select(study, id, arm)

pooled_subj_data <- DataSubject(
    data = pooled_subj_df,
    subject = "id",
    arm = "arm",
    study = "study"
)

pooled_long_df <- pooled_tumor_data |>
    select(id, year, sld)
pooled_long_data <- DataLongitudinal(
    data = pooled_long_df,
    formula = sld ~ year
)

pooled_surv_data <- DataSurvival(
    data = pooled_os_data,
    formula = Surv(os_time, os_event) ~ ecog + age + race + sex
)
pooled_joint_data <- DataJoint(
    subject = pooled_subj_data,
    longitudinal = pooled_long_data,
    survival = pooled_surv_data
)

So now we have pooled our 101 historical and 102 current patients into a single data set with 203 patients.

Fit the Bayesian hierarchical joint model

Now we can fit the Bayesian hierarchical joint model to the pooled data set, borrowing information from the historical data to inform the current data analysis.

Note that we use the same model specification historical_joint_mod as for the historical data only model fit above. The reason is that the LongitudinalSteinFojo class already accounts for hierarchical modeling, see the statistical specification here.

Show the code

save_file <- here("session-bhm/pooledmod1.rds")
if (file.exists(save_file)) {
    pooled_joint_results <- readRDS(save_file)
} else {
    pooled_joint_results <- sampleStanModel(
        historical_joint_mod,
        data = pooled_joint_data,
        iter_sampling = ITER,
        iter_warmup = WARMUP,
        chains = CHAINS,
        parallel_chains = CHAINS,
        thin = CHAINS,
        seed = BAYES.SEED,
        refresh = REFRESH
    )
    saveObject(pooled_joint_results, file = save_file)
}

Let’s first check again if the MCMC sampling went fine:

Show the code

mcmc_pooled_joint_results <- cmdstanr::as.CmdStanMCMC(pooled_joint_results)

mcmc_pooled_summary <- mcmc_pooled_joint_results$summary(vars)

print(mcmc_pooled_summary, n = 30)

# A tibble: 21 × 10
   variable           mean   median     sd    mad      q5     q95  rhat ess_bulk
   <chr>             <dbl>    <dbl>  <dbl>  <dbl>   <dbl>   <dbl> <dbl>    <dbl>
 1 lm_sf_mu_bsld…  3.76     3.76    0.0628 0.0613  3.65    3.86   1.05      134.
 2 lm_sf_mu_bsld…  3.77     3.77    0.0480 0.0454  3.69    3.85   1.02      234.
 3 lm_sf_mu_ks[1]  0.366    0.378   0.172  0.168   0.0676  0.622  1.00      540.
 4 lm_sf_mu_ks[2] -1.17    -1.15    0.335  0.321  -1.77   -0.680  1.00      685.
 5 lm_sf_mu_kg[1] -0.383   -0.379   0.120  0.122  -0.594  -0.194  1.00      486.
 6 lm_sf_mu_kg[2] -0.887   -0.884   0.133  0.137  -1.11   -0.669  1.00      624.
 7 lm_sf_sigma     4.26     4.26    0.132  0.133   4.06    4.49   1.00      756.
 8 lm_sf_omega_b…  0.577    0.575   0.0440 0.0423  0.512   0.653  1.00      314.
 9 lm_sf_omega_b…  0.487    0.486   0.0372 0.0369  0.430   0.551  1.01      535.
10 lm_sf_omega_k…  0.862    0.845   0.138  0.131   0.670   1.11   1.00      585.
11 lm_sf_omega_k…  1.52     1.49    0.267  0.244   1.14    1.99   0.999     632.
12 lm_sf_omega_k…  0.729    0.723   0.0855 0.0814  0.606   0.876  1.00      749.
13 lm_sf_omega_k…  0.954    0.948   0.0998 0.103   0.799   1.12   1.00      823.
14 beta_os_cov[1]  0.979    0.979   0.262  0.261   0.543   1.40   1.000    1019.
15 beta_os_cov[2] -0.00104 -0.00134 0.0112 0.0117 -0.0189  0.0176 0.998    1012.
16 beta_os_cov[3]  0.999    1.02    0.472  0.439   0.239   1.75   1.00      999.
17 beta_os_cov[4]  0.195    0.193   0.288  0.288  -0.247   0.673  1.00      946.
18 beta_os_cov[5]  0.234    0.237   0.246  0.241  -0.179   0.620  1.00     1033.
19 sm_weibull_ph…  1.81     1.80    0.176  0.170   1.52    2.10   1.00      934.
20 sm_weibull_ph…  0.248    0.195   0.188  0.135   0.0571  0.613  0.999     993.
21 link_growth     0.830    0.822   0.209  0.212   0.499   1.19   1.00      939.
# ℹ 1 more variable: ess_tail <dbl>

Indeed all rhat values are close to 1 indicating convergence.

Investigating the parameter estimates

We can see that now we have more model parameters, let’s see which are additional compared to the historical data only model:

Show the code

pooled_param_names <- mcmc_pooled_summary$variable
historical_param_names <- mcmc_historical_summary$variable
new_params <- setdiff(pooled_param_names, historical_param_names)
new_params

[1] "lm_sf_mu_bsld[2]"    "lm_sf_omega_bsld[2]"

We see that the additional parameters correspond to the baseline value, which is supposed to differ between studies: both the mean mu parameter and the standard deviation omega parameter gain an additional second dimension here with the addition of the second study.

Let’s look at the estimates of these new parameters and compare them between the studies:

Show the code

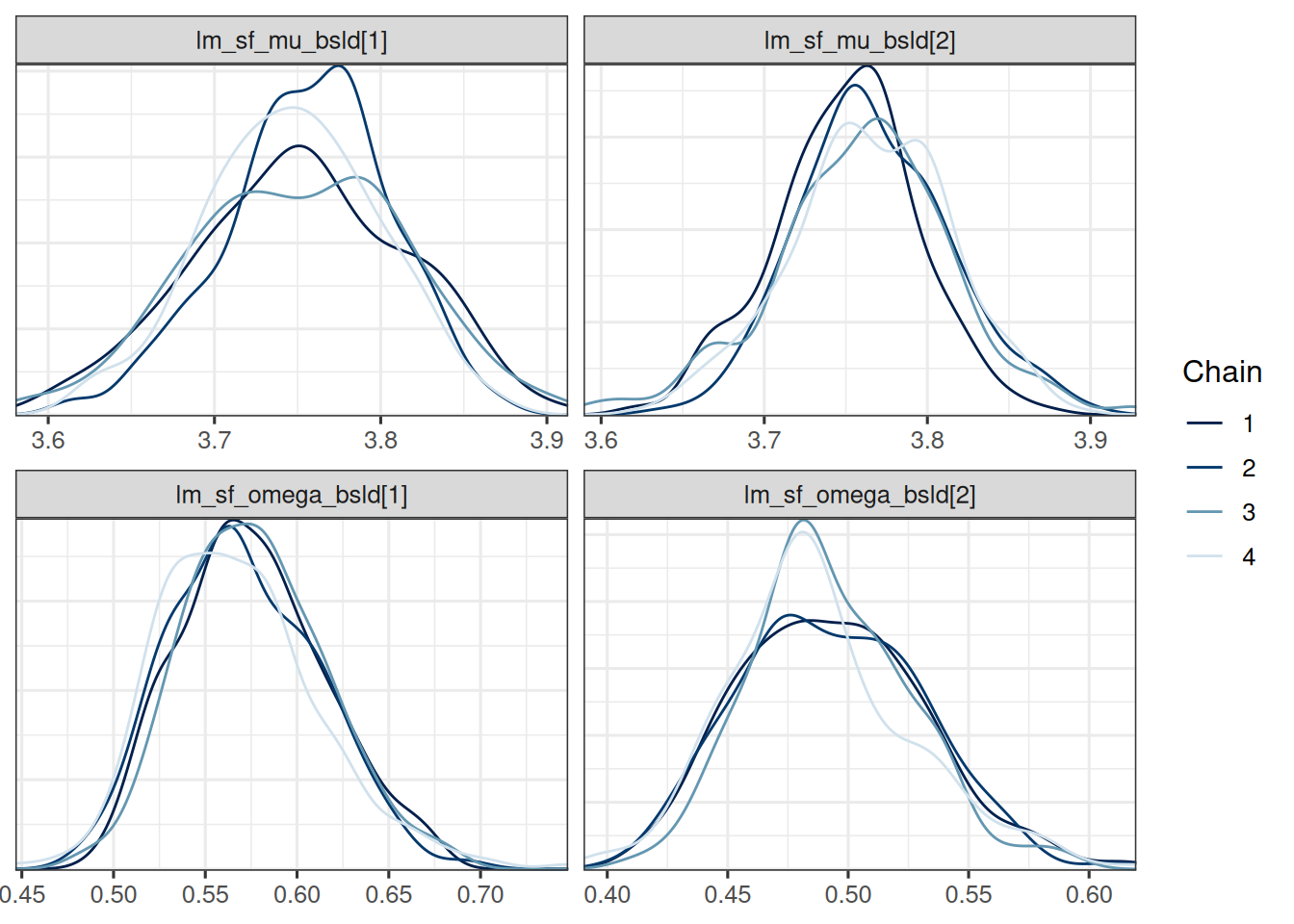
baseline_vars <- c("lm_sf_mu_bsld", "lm_sf_omega_bsld")
baseline_pooled_joint_results <- mcmc_pooled_joint_results$draws(baseline_vars)

mcmc_dens_overlay(baseline_pooled_joint_results)

Show the code

library(posterior)

# Convert draws to rvars for easier manipulation
baseline_rvars <- as_draws_rvars(baseline_pooled_joint_results)

mu_diff <- baseline_rvars$lm_sf_mu_bsld[1] - baseline_rvars$lm_sf_mu_bsld[2]
summary(mu_diff)

# A tibble: 1 × 10
  variable    mean  median     sd    mad     q5   q95  rhat ess_bulk ess_tail
  <chr>      <dbl>   <dbl>  <dbl>  <dbl>  <dbl> <dbl> <dbl>    <dbl>    <dbl>
1 mu_diff  -0.0165 -0.0153 0.0795 0.0754 -0.147 0.111  1.05     103.     233.

Show the code

omega_diff <- baseline_rvars$lm_sf_omega_bsld[1] - baseline_rvars$lm_sf_omega_bsld[2]
summary(omega_diff)

# A tibble: 1 × 10
  variable     mean median     sd    mad       q5   q95  rhat ess_bulk ess_tail
  <chr>       <dbl>  <dbl>  <dbl>  <dbl>    <dbl> <dbl> <dbl>    <dbl>    <dbl>
1 omega_diff 0.0897 0.0890 0.0565 0.0565 0.000180 0.187  1.00     372.     477.

As expected we don’t see a big difference in the baseline SLD between the historical and current study, neither in the mean nor in the standard deviation.

Sequential modeling approach

An alternative to fitting a Bayesian hierarchical joint model is to analyze the studies sequentially. We first fit a joint model to the historical study, as above, and use the posterior point estimates of its population-level parameters in the analysis of the current study. In the second fit these values are treated as known exactly: uncertainty from the historical analysis is not propagated to the current analysis, and the current data cannot update the fixed population-level parameters.

Here we use the posterior means from the historical fit for the Stein-Fojo population means (\(\mu\)) and standard deviations (\(\omega\)). The baseline parameters have one value per study, whereas the shrinkage and growth parameters have one value per treatment arm.

Show the code

population_vars <- c(
    "lm_sf_mu_bsld",
    "lm_sf_mu_ks",
    "lm_sf_mu_kg",
    "lm_sf_omega_bsld",
    "lm_sf_omega_ks",
    "lm_sf_omega_kg"
)

historical_population_summary <-
    mcmc_historical_joint_results$summary(population_vars)

get_posterior_means <- function(variable, summary) {
    rows <- summary$variable == variable |
        startsWith(summary$variable, paste0(variable, "["))
    summary$mean[rows]
}

historical_population_estimates <- setNames(
    lapply(
        population_vars,
        get_posterior_means,
        summary = historical_population_summary
    ),
    population_vars
)
historical_population_estimates

$lm_sf_mu_bsld
[1] 3.767197

$lm_sf_mu_ks
[1] -0.07633847 -1.14541681

$lm_sf_mu_kg
[1] -0.5919843 -0.8631262

$lm_sf_omega_bsld
[1] 0.4841961

$lm_sf_omega_ks
[1] 1.045875 1.534105

$lm_sf_omega_kg
[1] 0.4949692 1.0242679

Show the code

historical_arm_names <- names(
    as_stan_list(historical_subj_data)$arm_to_index
)

# The order in this table is the order required by prior_const_vector().
historical_arm_order <- tibble(
    arm_index = seq_along(historical_arm_names),
    arm = historical_arm_names
)

historical_baseline_estimates <- tibble(
    parameter = c("lm_sf_mu_bsld", "lm_sf_omega_bsld"),
    arm_index = NA_integer_,
    arm = "historical",
    estimate = unlist(historical_population_estimates[c(
        "lm_sf_mu_bsld", "lm_sf_omega_bsld"
    )])
)

historical_mu_ks_estimates <- historical_arm_order |>
    mutate(
        parameter = "lm_sf_mu_ks",
        estimate = historical_population_estimates$lm_sf_mu_ks
    )

historical_mu_kg_estimates <- historical_arm_order |>
    mutate(
        parameter = "lm_sf_mu_kg",
        estimate = historical_population_estimates$lm_sf_mu_kg
    )

historical_omega_ks_estimates <- historical_arm_order |>
    mutate(
        parameter = "lm_sf_omega_ks",
        estimate = historical_population_estimates$lm_sf_omega_ks
    )

historical_omega_kg_estimates <- historical_arm_order |>
    mutate(
        parameter = "lm_sf_omega_kg",
        estimate = historical_population_estimates$lm_sf_omega_kg
    )

historical_population_estimates_df <- bind_rows(
    historical_baseline_estimates,
    historical_mu_ks_estimates,
    historical_mu_kg_estimates,
    historical_omega_ks_estimates,
    historical_omega_kg_estimates
)

historical_population_estimates_df

# A tibble: 10 × 4
   parameter        arm_index arm        estimate
   <chr>                <int> <chr>         <dbl>
 1 lm_sf_mu_bsld           NA historical   3.77  
 2 lm_sf_omega_bsld        NA historical   0.484 
 3 lm_sf_mu_ks              1 Docetaxel   -0.0763
 4 lm_sf_mu_ks              2 MPDL3280A   -1.15  
 5 lm_sf_mu_kg              1 Docetaxel   -0.592 
 6 lm_sf_mu_kg              2 MPDL3280A   -0.863 
 7 lm_sf_omega_ks           1 Docetaxel    1.05  
 8 lm_sf_omega_ks           2 MPDL3280A    1.53  
 9 lm_sf_omega_kg           1 Docetaxel    0.495 
10 lm_sf_omega_kg           2 MPDL3280A    1.02

Next we create the joint-model data object for the current study only.

Show the code

current_subj_df <- current_os_data |>
    select(study, id, arm)
current_subj_data <- DataSubject(
    data = current_subj_df,
    subject = "id",
    arm = "arm",
    study = "study"
)
current_arm_names <- names(
    as_stan_list(current_subj_data)$arm_to_index
)
stopifnot(identical(current_arm_names, historical_arm_names))

current_long_df <- current_tumor_data |>
    select(id, year, sld)
current_long_data <- DataLongitudinal(
    data = current_long_df,
    formula = sld ~ year
)

current_surv_data <- DataSurvival(
    data = current_os_data,
    formula = Surv(os_time, os_event) ~ ecog + age + race + sex
)

current_joint_data <- DataJoint(
    subject = current_subj_data,
    longitudinal = current_long_data,
    survival = current_surv_data
)

We then specify a constant (also called Dirac or point-mass) prior for each of the six historical population estimates. prior_const() supplies the single historical-study value for each baseline parameter; because the current data also contain one study, jmpost replicates that scalar to the parameter’s study dimension. prior_const_vector() supplies the arm-specific shrinkage and growth parameters in the order shown by historical_arm_order: arm_index = 1 is the first vector element, arm_index = 2 is the second, and so on. We verify below that the current-study data use this same order. The subject-level random effects and the remaining joint-model parameters are still estimated from the current data, conditional on these fixed population values.

Show the code

current_sequential_mod <- JointModel(
    longitudinal = LongitudinalSteinFojo(
        mu_bsld = prior_const(
            historical_population_estimates$lm_sf_mu_bsld
        ),
        mu_ks = prior_const_vector(
            historical_population_estimates$lm_sf_mu_ks
        ),
        mu_kg = prior_const_vector(
            historical_population_estimates$lm_sf_mu_kg
        ),
        omega_bsld = prior_const(
            historical_population_estimates$lm_sf_omega_bsld
        ),
        omega_ks = prior_const_vector(
            historical_population_estimates$lm_sf_omega_ks
        ),
        omega_kg = prior_const_vector(
            historical_population_estimates$lm_sf_omega_kg
        ),
        sigma = prior_normal(0, 3) |> set_limits(0, Inf)
    ),
    survival = SurvivalWeibullPH(
        lambda = prior_gamma(0.7, 1),
        gamma = prior_gamma(1.5, 1),
        beta = prior_normal(0, 20)
    ),
    link = linkGrowth(
        prior = prior_normal(0, 20)
    )
)

Now we fit this model to the current data only.

Show the code

save_file <- here("session-bhm/currentmod_sequential1.rds")
if (file.exists(save_file)) {
    current_sequential_results <- readRDS(save_file)
} else {
    current_sequential_results <- sampleStanModel(
        current_sequential_mod,
        data = current_joint_data,
        iter_sampling = ITER,
        iter_warmup = WARMUP,
        chains = CHAINS,
        parallel_chains = CHAINS,
        thin = CHAINS,
        seed = BAYES.SEED,
        refresh = REFRESH
    )
    saveObject(current_sequential_results, file = save_file)
}

Investigating the current-data parameter estimates

As before, we inspect the posterior summary of the fitted model. An NA value for rhat is expected for a fixed parameter: To see this, start from the fact that all its draws are identical, so the between- and within-chain variances \(B\) and \(W\), as well as \(s_m^2\) for all chains \(m\), defined in the Stan manual here are all zero. Therefore the variance estimator \(\widehat{\textrm{var}}^{+}\) defined in the Stan manual here is also zero. Hence the \(\hat{R}\) estimator, defined as the square root of \(\widehat{\textrm{var}}^{+}\) and \(W\), is undefined. Finally, the effective sample size defined in the Stan manual here is undefined, because it depends on the autocorrelation estimates at lag \(t\), \(\hat{\rho}_{t}\), which are undefined because they are calculated as one minus a fraction, which is zero divided by zero in this case.

Show the code

mcmc_current_sequential_results <-
    cmdstanr::as.CmdStanMCMC(current_sequential_results)

current_sequential_summary <-
    mcmc_current_sequential_results$summary(vars)

print(current_sequential_summary, n = 30)

# A tibble: 19 × 10
   variable          mean  median     sd    mad      q5      q95   rhat ess_bulk
   <chr>            <dbl>   <dbl>  <dbl>  <dbl>   <dbl>    <dbl>  <dbl>    <dbl>
 1 lm_sf_mu_bsld…  3.77    3.77   0      0       3.77    3.77    NA          NA 
 2 lm_sf_mu_ks[1] -0.0763 -0.0763 0      0      -0.0763 -0.0763  NA          NA 
 3 lm_sf_mu_ks[2] -1.15   -1.15   0      0      -1.15   -1.15    NA          NA 
 4 lm_sf_mu_kg[1] -0.592  -0.592  0      0      -0.592  -0.592   NA          NA 
 5 lm_sf_mu_kg[2] -0.863  -0.863  0      0      -0.863  -0.863   NA          NA 
 6 lm_sf_sigma     3.90    3.90   0.203  0.210   3.56    4.24     1.01      284.
 7 lm_sf_omega_b…  0.484   0.484  0      0       0.484   0.484   NA          NA 
 8 lm_sf_omega_k…  1.05    1.05   0      0       1.05    1.05    NA          NA 
 9 lm_sf_omega_k…  1.53    1.53   0      0       1.53    1.53    NA          NA 
10 lm_sf_omega_k…  0.495   0.495  0      0       0.495   0.495   NA          NA 
11 lm_sf_omega_k…  1.02    1.02   0      0       1.02    1.02    NA          NA 
12 beta_os_cov[1]  0.794   0.772  0.453  0.457   0.0821  1.57     1.00      941.
13 beta_os_cov[2] -0.0180 -0.0186 0.0146 0.0153 -0.0404  0.00747  1.00     1115.
14 beta_os_cov[3]  1.77    1.72   0.888  0.836   0.340   3.25     0.999     815.
15 beta_os_cov[4]  0.362   0.342  0.497  0.479  -0.395   1.23     0.999     931.
16 beta_os_cov[5]  0.0941  0.0942 0.395  0.383  -0.572   0.789    1.00     1016.
17 sm_weibull_ph…  2.63    2.62   0.408  0.394   1.98    3.31     0.999     888.
18 sm_weibull_ph…  1.21    0.950  0.918  0.719   0.221   3.12     1.00     1113.
19 link_growth     1.25    1.19   0.434  0.411   0.635   1.96     1.01      434.
# ℹ 1 more variable: ess_tail <dbl>

Finally, we compare uncertainty in parameters that were not fixed in the sequential fit. We focus on the survival covariate effects, the Weibull scale parameter, and the tumor-growth link parameter:

beta_os_cov: survival covariate effects
sm_weibull_ph_lambda: Weibull scale parameter
link_growth: association between tumor growth and survival

For each parameter, we extract the posterior mean and standard deviation from both fits. The ratio in the final column is below 1 when the sequential fit has the smaller posterior standard deviation.

Show the code

comparison_vars <- c(
    "beta_os_cov",
    "sm_weibull_ph_lambda",
    "link_growth"
)

bhjm_parameter_summary <- mcmc_pooled_joint_results$summary(
    comparison_vars
) |>
    transmute(
        parameter = variable,
        bhjm_mean = mean,
        bhjm_sd = sd
    )

sequential_parameter_summary <- mcmc_current_sequential_results$summary(
    comparison_vars
) |>
    transmute(
        parameter = variable,
        sequential_mean = mean,
        sequential_sd = sd
    )

parameter_uncertainty_comparison <- left_join(
    bhjm_parameter_summary,
    sequential_parameter_summary,
    by = "parameter"
) |>
    mutate(
        sequential_to_bhjm_sd = sequential_sd / bhjm_sd
    )

parameter_uncertainty_comparison

# A tibble: 7 × 6
  parameter            bhjm_mean bhjm_sd sequential_mean sequential_sd
  <chr>                    <dbl>   <dbl>           <dbl>         <dbl>
1 beta_os_cov[1]         0.979    0.262           0.794         0.453 
2 beta_os_cov[2]        -0.00104  0.0112         -0.0180        0.0146
3 beta_os_cov[3]         0.999    0.472           1.77          0.888 
4 beta_os_cov[4]         0.195    0.288           0.362         0.497 
5 beta_os_cov[5]         0.234    0.246           0.0941        0.395 
6 sm_weibull_ph_lambda   0.248    0.188           1.21          0.918 
7 link_growth            0.830    0.209           1.25          0.434 
# ℹ 1 more variable: sequential_to_bhjm_sd <dbl>

In this example, interestingly the sequential fit has larger posterior standard deviations for the non-fixed parameters shown above. The two fits also use different outcome data—the BHJM uses both studies, whereas the second-stage sequential model uses only the current study—so the direction and size of the difference can vary across parameters. The BHJM propagates uncertainty about the population parameters instead of treating their historical estimates as known with certainty.

Goodness of fit

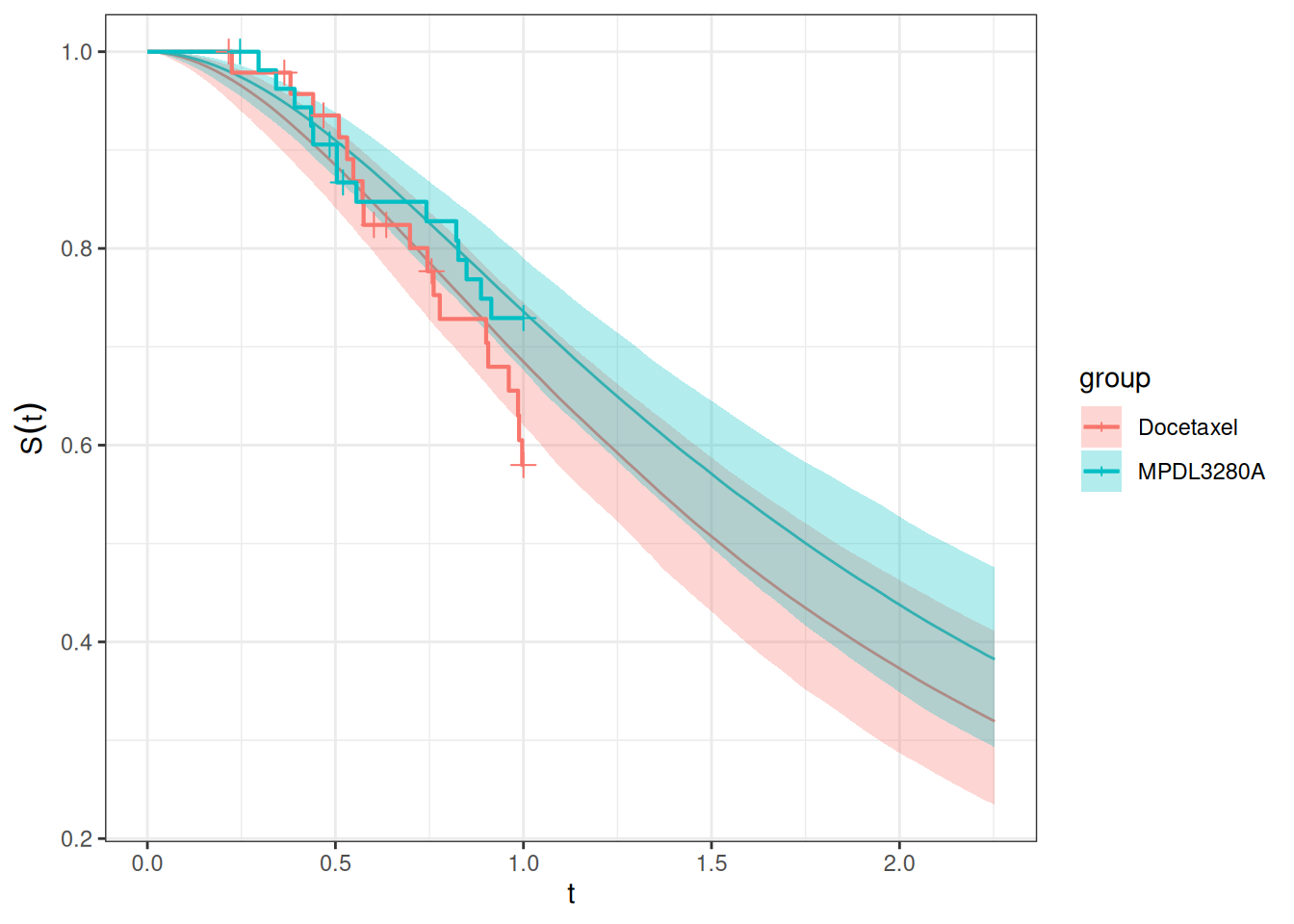
Let’s check the goodness of fit to our current study data:

Show the code

current_subj_df <- current_os_data |>
    select(study, id, arm)

time_grid <- seq(from = 0, to = max(pooled_os_data$os_time), length = 100)
current_os_surv_group_grid <- GridGrouped(
    times = time_grid,
    groups = with(
        current_subj_df,
        split(as.character(id), arm)
    )
)
current_os_surv_pred <- SurvivalQuantities(
    object = pooled_joint_results,
    grid = current_os_surv_group_grid,
    type = "surv"
)

autoplot(current_os_surv_pred, add_km = TRUE, add_wrap = FALSE)

So the fit looks satisfactory, considering that the current data are quite immature.

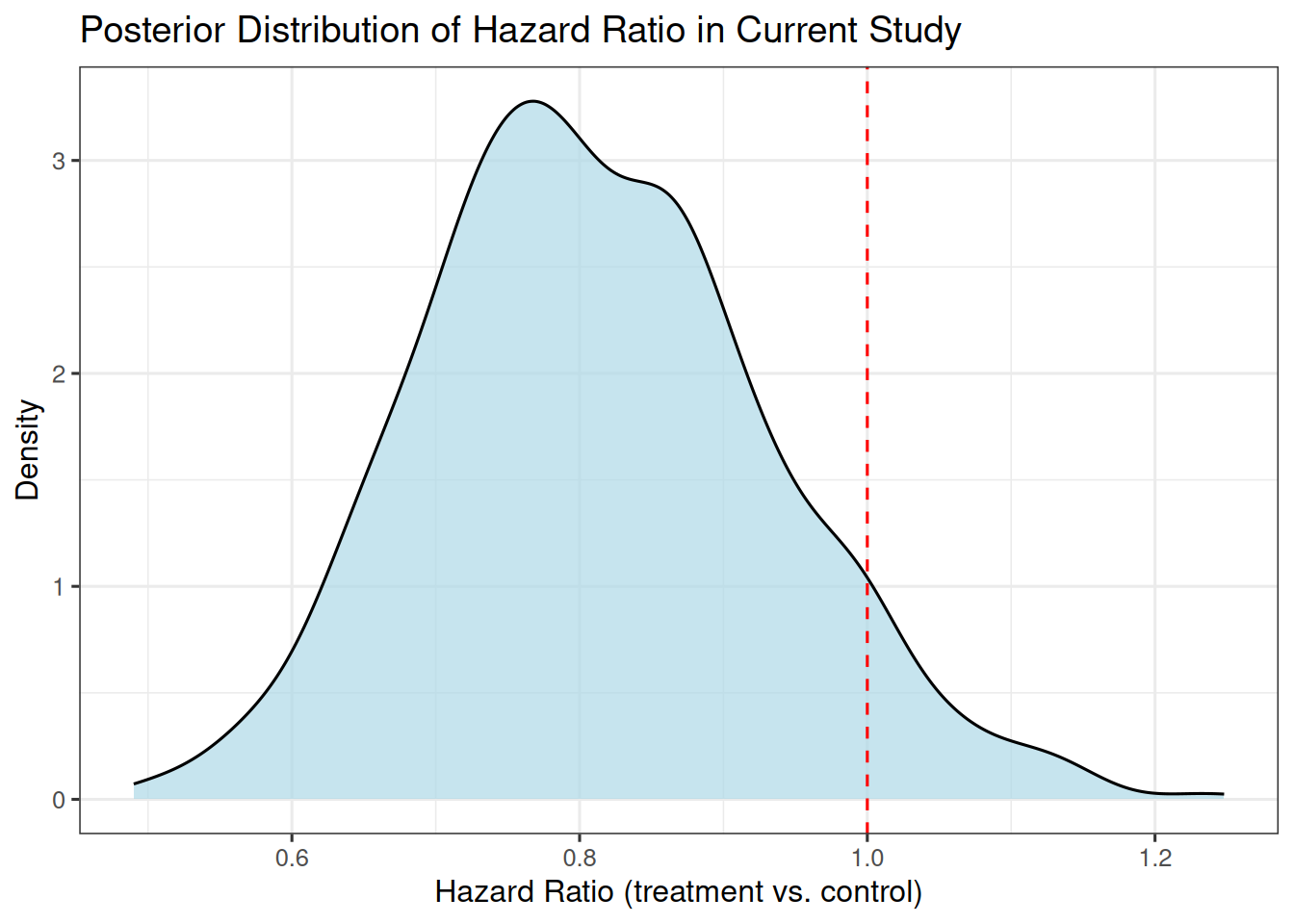
Posterior distribution of the hazard ratio

Now let’s look at the posterior distribution of the hazard ratio between the two treatment arms in the current study. We do this as follows:

For a given MCMC sample \(i\):
- Sample predicted survival times for the current study subjects which are still being followed up
- Fit a Cox proportional hazards regression model
- Extract the hazard ratio estimate
Repeat for all MCMC samples to get the posterior distribution of the hazard ratio

This is the same algorithm we used in the session 4 here.

In this example we assume for simplicity:

no additional patients will be enrolled, i.e. we don’t need to add new patients to the data set
all currently censored patients will be followed up until event occurs

Therefore we can directly jump into the sampling step as described here:

Show the code

# Determine for which patients we want to sample the individual survival times.
pt_to_sample <- pooled_os_data |>
    filter(study == "current" & os_event == 0)
pt_to_sample_ids <- pt_to_sample$id

# Obtain the survival function samples (for all patients here).
length_time_grid <- 100
time_grid_end <- round(max(pooled_os_data$os_time) + 10, 1)
time_grid <- seq(0, time_grid_end, length = length_time_grid)

save_file <- here("session-bhm/bhm1_surv_samples.rds")
if (file.exists(save_file)) {
    os_surv_samples <- readRDS(save_file)
} else {
    os_surv_samples <- SurvivalQuantities(
        object = pooled_joint_results,
        grid = GridFixed(times = time_grid),
        type = "surv"
    )
    saveRDS(os_surv_samples, file = save_file)
}

qs <- os_surv_samples@quantities
include_qs <- qs@groups %in% pt_to_sample_ids

qs_samples <- qs@quantities[, include_qs]
qs_times <- qs@times[include_qs]
qs_groups <- qs@groups[include_qs]

surv_values_samples <- matrix(
    qs_samples,
    nrow = ITER * length(pt_to_sample_ids),
    ncol = length_time_grid
)

surv_values_pt_ids <- rep(
    head(qs_groups, length(pt_to_sample_ids)),
    each = ITER
)

censoring_times <- pt_to_sample$os_time[match(
    surv_values_pt_ids,
    pt_to_sample_ids
)]

library(Rcpp)

# Use Rcpp function for single patient, single sample.
sourceCpp(here("session-pts/conditional_sampling.cpp"))

cond_surv_time_samples <- sample_conditional_survival_times(
    time_grid = time_grid,
    surv_values = surv_values_samples,
    censoring_times = censoring_times
)

os_cond_samples <- matrix(
    cond_surv_time_samples$t_results,
    nrow = ITER,
    ncol = length(pt_to_sample_ids),
    dimnames = list(seq_len(ITER), head(qs_groups, length(pt_to_sample_ids)))
)

The next step is again to create the complete OS data sets. Here we just use the current data set and replace the censored times with the sampled times above:

Show the code

os_rows_to_replace <- match(
    pt_to_sample_ids,
    current_os_data$id
)

os_cond_samples_cols <- match(
    pt_to_sample_ids,
    colnames(os_cond_samples)
)

os_data_samples <- lapply(1:ITER, function(i) {
    # Create a copy of the original OS data
    os_data_sample <- current_os_data[, c("id", "arm", "os_time", "os_event", "race", "sex", "ecog", "age")]

    # Add the sampled OS times for the patients who are still being followed up.
    os_data_sample$os_time[os_rows_to_replace] <- os_cond_samples[
        i,
        os_cond_samples_cols
    ]

    # Set the OS event to TRUE for those patients, because we assume they have an event now.
    os_data_sample$os_event[os_rows_to_replace] <- TRUE

    os_data_sample
})

Now we can fit a Cox proportional hazards regression model to each of the completed data sets and extract the hazard ratio estimates:

Show the code

hr_est_fun <- function(df) {
    cox_mod <- coxph(Surv(os_time, os_event) ~ arm,
        data = df
    )
    exp(unname(coef(cox_mod)))
}

We can try on one data set first:

Show the code

hr_est_fun(os_data_samples[[1]])

[1] 0.8164386

Now we can apply this to all data sets:

Show the code

hr_estimates <- sapply(os_data_samples, hr_est_fun)

We can visualize this:

Show the code

library(ggplot2)
hr_df <- data.frame(hr = hr_estimates)
ggplot(hr_df, aes(x = hr)) +
    geom_density(fill = "lightblue", alpha = 0.7) +
    geom_vline(xintercept = 1, linetype = "dashed", color = "red") +
    xlab("Hazard Ratio (treatment vs. control)") +
    ylab("Density") +
    ggtitle("Posterior Distribution of Hazard Ratio in Current Study")

Probability of success

Let’s assume the minimal detectable difference, i.e. the hazard ratio that we would consider clinically relevant, is 0.75. Then our probability of success is given by the posterior probability that the hazard ratio is below 0.75:

Show the code

mean(hr_estimates < 0.75)

[1] 0.502