---
title: "1. Calculate Bayesian Predictive Power"
author:
- Daniel Sabanés Bové
- Francois Mercier
date: last-modified
editor_options:
chunk_output_type: inline
format:
html:
code-fold: show
html-math-method: mathjax
cache: true
---
The purpose of this document is to show how we can calculate the probability of success given interim data of a clinical trial, based on the TGI-OS joint model results.
## Setup and load data
Here we execute the R code from the setup and data preparation chapter, see the [full code here](0_setup.qmd).
```{r}
#| label: setup_and_load_data
#| echo: false
#| output: false
library(here)
options(knitr.duplicate.label = "allow")
knitr::purl(
here("session-pts/_setup.qmd"),
output = here("session-pts/_setup.R")
)
source(here("session-pts/_setup.R"))
knitr::purl(
here("session-pts/_load_data.qmd"),
output = here("session-pts/_load_data.R")
)
source(here("session-pts/_load_data.R"))
```
## Fit our joint TGI-OS model
Let's fit again the same joint TGI-OS model as in the previous session. Now we just put all the code together in a single chunk, and it is a good repetition to see all the steps in one place:
```{r}
#| label: fit_joint_model
subj_df <- os_data |>
mutate(study = "OAK") |>
select(study, id, arm)
subj_data <- DataSubject(
data = subj_df,
subject = "id",
arm = "arm",
study = "study"
)
long_df <- tumor_data |>
select(id, year, sld)
long_data <- DataLongitudinal(
data = long_df,
formula = sld ~ year
)
surv_data <- DataSurvival(
data = os_data,
formula = Surv(os_time, os_event) ~ ecog + age + race + sex
)
joint_data <- DataJoint(
subject = subj_data,
longitudinal = long_data,
survival = surv_data
)
joint_mod <- JointModel(
longitudinal = LongitudinalSteinFojo(
mu_bsld = prior_normal(log(65), 1),
mu_ks = prior_normal(log(0.52), 1),
mu_kg = prior_normal(log(1.04), 1),
omega_bsld = prior_normal(0, 3) |> set_limits(0, Inf),
omega_ks = prior_normal(0, 3) |> set_limits(0, Inf),
omega_kg = prior_normal(0, 3) |> set_limits(0, Inf),
sigma = prior_normal(0, 3) |> set_limits(0, Inf)
),
survival = SurvivalWeibullPH(
lambda = prior_gamma(0.7, 1),
gamma = prior_gamma(1.5, 1),
beta = prior_normal(0, 20)
),
link = linkGrowth(
prior = prior_normal(0, 20)
)
)
options("jmpost.prior_shrinkage" = 0.99)
# initialValues(joint_mod, n_chains = CHAINS)
save_file <- here("session-pts/jm1.rds")
if (file.exists(save_file)) {
joint_results <- readRDS(save_file)
} else {
joint_results <- sampleStanModel(
joint_mod,
data = joint_data,
iter_sampling = ITER,
iter_warmup = WARMUP,
chains = CHAINS,
parallel_chains = CHAINS,
thin = CHAINS,
seed = BAYES.SEED,
refresh = REFRESH
)
saveObject(joint_results, file = save_file)
}
```
## Marginal Hazard Ratio Estimation
First, we will try to apply the methodology from [Oudenhoven et al (2020)](https://onlinelibrary.wiley.com/doi/10.1002/sim.8713) to estimate the marginal hazard ratio, using our joint model results.
We use the new `jmpost` function called `populationHR()` for this:
```{r}
#| label: calculate_marginal_hr
save_file <- here("session-pts/jm1hr.rds")
if (file.exists(save_file)) {
pop_hr <- readRDS(save_file)
} else {
pop_hr <- populationHR(
joint_results,
hr_formula = ~arm
)
saveRDS(pop_hr, file = save_file)
}
pop_hr$summary
```
So here we have the marginal log hazard ratio estimates of the baseline spline components and the treatment arm.
Therefore we can get the hazard ratio estimates by exponentiating the log hazard ratio estimates:
```{r}
#| label: exponentiate_hr_estimates
hr_est <- pop_hr$summary["armMPDL3280A", ] |>
sapply(exp)
```
So we get a marginal hazard ratio estimate of around `r round(hr_est["mean"], 3)` and a 95% credible interval of `r paste0(signif(hr_est[c("X2.5.", "X97.5.")], 2), collapse = " - ")`.
## Comparison with simple Cox PH results
We can do a little sanity check by comparing this with a very simple Cox model:
```{r}
#| label: cox_model_comparison
cox_mod <- survival::coxph(
update(joint_results@data@survival@formula, ~ . + arm),
data = joint_results@data@survival@data
)
summary(cox_mod)
```
Here we get a different HR estimate of around `r round(exp(coef(cox_mod)["armMPDL3280A"]), 2)`, which is lower than the one we got from the joint model.
We should expect different results because the joint model takes into account the TGI effect, while the Cox model does not.
And if we just put the treatment arm into the Cox model we get:
```{r}
#| label: cox_model_arm_only
cox_mod_arm <- survival::coxph(
update(joint_results@data@survival@formula, . ~ arm),
data = joint_results@data@survival@data
)
cox_mod_arm
```
Here we get a HR of `r round(exp(coef(cox_mod_arm)["armMPDL3280A"]), 3)` that is close to the marginal HR estimate above (when we did not condition on the other covariates), which is reassuring.
On the other hand, the 95% confidence interval is:
```{r}
#| label: cox_confidence_interval
exp(confint(cox_mod_arm)["armMPDL3280A", ])
```
so actually overlaps the null hypothesis of 1. So we see that the joint model helped us to obtain a more precise estimate of the marginal hazard ratio.
## PTS based on frequentist HR properties
From now on we pretend that the data we have analyzed so far is the interim data of the Oak trial, and we want to calculate the predictive power of the trial based on this interim data.
Let's first try to use the log HR ($\delta$) frequentist distribution to calculate the predictive power of the trial. We have:
$$
\hat{\delta}_{\text{fin}} \vert \hat{\delta}_{\text{int}}
\sim
\text{Normal}(\hat{\delta}_{\text{int}}, \sigma^2_{\text{int}})
$$
where the predictive variance is given by
$$
\sigma^2_{\text{int}} = \frac{1}{4\overline{p}r(1-r)} \frac{\overline{m}}{\overline{n} (\overline{n} + \overline{m})}
$$
On the other hand, assuming that we have observed the final data, then the variance estimate for the estimator $\hat{\delta}_{\text{fin}}$ is given by:
$$
\sigma^2_{\text{fin}} = \frac{1}{4\overline{p}r(1-r)} \frac{1}{\overline{n} + \overline{m}}
$$
So the $(1-\alpha)$-confidence interval for the final log HR is given by:
$$
\hat{\delta}_{\text{fin}} \pm z_{1 - \alpha/2} \sigma_{\text{fin}}
$$
and the null hypothesis is rejected if the upper bound of this confidence interval is below 0, i.e. if:
$$
\hat{\delta}_{\text{fin}} + z_{1 - \alpha/2} \sigma_{\text{fin}} < 0.
$$
Now let's again take the perspective that we are at the interim analysis and we want to calculate the predictive probability of this event, then:
$$
\begin{align*}
\mathbb{P}(\hat{\delta}_{\text{fin}} + z_{1 - \alpha/2} \sigma_{\text{fin}} < 0)
&=
\mathbb{P}(\hat{\delta}_{\text{fin}} < - z_{1 - \alpha/2} \sigma_{\text{fin}}) \\
&=
\mathbb{P}\left(
\frac{\hat{\delta}_{\text{fin}} - \hat{\delta}_{\text{int}}}{\sigma_{\text{int}}} <
\frac{- z_{1 - \alpha/2} \sigma_{\text{fin}} - \hat{\delta}_{\text{int}}}{\sigma_{\text{int}}}
\right) \\
&=
\Phi\left(
\frac{- z_{1 - \alpha/2} \sigma_{\text{fin}} - \hat{\delta}_{\text{int}}}{\sigma_{\text{int}}}
\right)
\end{align*}
$$
because the left-hand side is a standard normal variable according to our formula above.
Let's first write a little function to calculate this:
```{r}
#| label: pts_freq_hr_function
pts_freq_hr <- function(delta_int, var_int, var_final, alpha = 0.05) {
z_alpha <- qnorm(1 - alpha / 2)
delta_final <- -z_alpha * sqrt(var_final)
pnorm((delta_final - delta_int) / sqrt(var_int))
}
```
For $\hat{\delta}_{\text{int}}$ we are going to plug in our MCMC samples for the marginal log HR $\hat{\delta}_{\text{int}}$ to compute the PTS based on this:
```{r}
#| label: extract_log_hr_samples
log_hr_samples <- pop_hr[[2]]["armMPDL3280A", ]
```
But first we also need the quantities that go into the variance formula:
- $\overline{p}$: average event rate
- $r$: proportion of patients in the treatment arm
- $\overline{n}$: average arm size in interim data
- $\overline{m}$: average arm size in follow up
So let's calculate these and the resulting variances:
```{r}
#| label: calculate_variance_quantities
avg_event_rate <- mean(os_data$os_event)
prop_pts_treatment <- mean(os_data$arm == "MPDL3280A")
avg_arm_size_interim <- mean(table(os_data$arm))
total_size_final <- 850
avg_arm_size_followup <- (total_size_final - 2 * avg_arm_size_interim) / 2
var_int <- 1 /
(4 * avg_event_rate * prop_pts_treatment * (1 - prop_pts_treatment)) *
avg_arm_size_followup /
(avg_arm_size_interim * (avg_arm_size_interim + avg_arm_size_followup))
var_final <- 1 /
(4 * avg_event_rate * prop_pts_treatment * (1 - prop_pts_treatment)) *
1 /
(avg_arm_size_interim + avg_arm_size_followup)
```
Now we can calculate the PTS based on the frequentist HR properties:
```{r}
#| label: calculate_pts_freq_hr
pts_freq_hr_result <- mean(pts_freq_hr(
delta_int = log_hr_samples,
var_int = var_int,
var_final = var_final
))
pts_freq_hr_result
```
So we obtain a PTS of `r round(pts_freq_hr_result * 100, 1)`% here.
## PTS based on frequentist log-rank test properties
Now we want to leverage the `rpact` function [`getConditionalPower()`](https://rpact-com.github.io/rpact/reference/getConditionalPower.html) to calculate the predictive power of the trial based on the log-rank test statistic properties.
Looking at the function's example, we first have to create a `DataSet` object with the interim data.
Here it is important that we for `cumLogRanks` also the z scores from a Cox regression can be used, which means for our case that can insert here the z-scores defined as:
$$
z = \frac{\hat{\delta}_{\text{int}}}{\sigma_{\text{int}}}
$$
values.
But let's first try this with a simple fixed $z$ value to see how it works:
```{r}
#| label: rpact_dataset_example
library(rpact)
z <- log(0.9) / sqrt(var_int) # Instead of log(0.9) we put later the marginal log HR MCMC sample
data <- getDataset(
cumEvents = sum(os_data$os_event),
cumLogRanks = z,
cumAllocationRatios = prop_pts_treatment
)
data
```
This is the data set from the first stage, i.e. our interim analysis.
Now we need to define the design of the group sequential trial:
```{r}
#| label: define_group_sequential_design
events_final <- total_size_final * avg_event_rate
design <- getDesignGroupSequential(
kMax = 2,
informationRates = c(sum(os_data$os_event) / events_final, 1),
alpha = 0.05
)
design
```
We see that the significance level is almost full for the final analysis, because by default the O'Brien & Fleming design is used, which only assigns a very small $\alpha$ to the interim analysis. This is kind of what we need here.
Finally we put the `design` and `data` in a `StageResults` object, which is the input for the `getConditionalPower()` function:
```{r}
#| label: calculate_conditional_power
stageResults <- getStageResults(
design = design,
dataInput = data,
stage = 1,
directionUpper = FALSE
)
condPower <- getConditionalPower(
stageResults = stageResults,
thetaH1 = 0.9, # Here we put later the marginal hazard ratio MCMC sample
nPlanned = total_size_final,
allocationRatioPlanned = 1
)
summary(condPower)
condPower$conditionalPower[2]
```
OK so now that we know how it works we wrap this in a little function again.
```{r}
#| label: pts_freq_hr2_function
pts_freq_hr2 <- function(
delta_int,
var_int,
var_final,
events_int,
alloc_int,
events_final,
alpha = 0.05) {
data <- getDataset(
cumEvents = events_int,
cumLogRanks = delta_int / sqrt(var_int),
cumAllocationRatios = alloc_int
)
design <- getDesignGroupSequential(
kMax = 2,
informationRates = c(events_int / events_final, 1),
alpha = alpha
)
stageResults <- getStageResults(
design = design,
dataInput = data,
stage = 1,
directionUpper = FALSE
)
condPower <- getConditionalPower(
stageResults = stageResults,
thetaH1 = exp(delta_int),
nPlanned = total_size_final,
allocationRatioPlanned = 1
)
condPower$conditionalPower[2]
}
```
Let's try it out with the same example first again:
```{r}
#| label: test_pts_freq_hr2
pts_freq_hr2(
delta_int = log(0.9),
var_int = var_int,
var_final = var_final,
events_int = sum(os_data$os_event),
alloc_int = prop_pts_treatment,
events_final = total_size_final * avg_event_rate
)
```
OK so that gives the same result as before, which is good. Now we can plug in the MCMC samples for the marginal log HR:
```{r}
#| label: calculate_pts_freq_hr2
save_file <- here("session-pts/jm1hr2.rds")
if (file.exists(save_file)) {
pts_freq_hr2_samples <- readRDS(save_file)
} else {
pts_freq_hr2_samples <- sapply(
log_hr_samples,
pts_freq_hr2,
var_int = var_int,
var_final = var_final,
events_int = sum(os_data$os_event),
alloc_int = prop_pts_treatment,
events_final = total_size_final * avg_event_rate
)
saveRDS(pts_freq_hr2_samples, file = save_file)
}
pts_freq_hr2_result <- mean(pts_freq_hr2_samples)
pts_freq_hr2_result
```
So here we get a PTS of `r round(pts_freq_hr2_result * 100, 1)`%, which is higher than the one we got before.
## Individual Samples based Predictive Power
This is a good motivation to try out the conditional sampling approach to calculate the predictive power, which is based on the individual samples of the joint model. It does not involved any frequentist assumptions to calculate the PTS.
We will perform the following steps in this algorithm:
1. We add as many new patients to the survival data set as we expect to still enter the trial.
- These patients have survival time 0 and are censored at that time, which means they are completely new patients.
1. We refit the joint model with this augmented data set. This simplifies the subsequent sampling process.
1. For each patient who is still being followed up for OS at IA (=does not have an event yet and did not drop out)
- Obtain individual survival distribution MCMC samples over a long enough time grid
- Condition on last observed censored OS time, sample once per MCMC sample from the conditional survival distribution
1. Define "End of Study" time, e.g. based on number of events observed, calendar time, etc.
1. Apply summary statistic of interest to the complete "End of Study" OS data set samples and aggregate appropriately
- For example, we can use the log-rank test statistic as summary statistic
1. Calculate the proportion of samples that are above the critical value for the summary statistic, e.g. log-rank test statistic
Note that for the first step, we need to add some random information to the data set, because unfortunately the real data does not differentiate between patients who are still being followed up and those who have dropped out.
### Add new patients and generate random lost-to-follow-up flag
Basically for those patients with a censored survival time, we randomly assign a lost-to-follow-up flag with a probability of 10%, so that we can simulate some patients who are still being followed up and some who are not. We sample the covariates from the distribution of the already observed patients.
```{r}
#| label: generate_lost_to_follow_up
set.seed(689)
lost_to_follow_up_flag <- sample(
c(TRUE, FALSE),
size = nrow(os_data),
replace = TRUE,
prob = c(0.1, 0.9)
)
os_data <- os_data |>
mutate(lost_to_follow_up = !os_event & lost_to_follow_up_flag)
n_lost_to_follow_up <- sum(os_data$lost_to_follow_up)
n_lost_to_follow_up
set.seed(359)
n_new_patients <- 2 * avg_arm_size_followup
os_data_new <- data.frame(
id = seq(from = max(as.integer(as.character(os_data$id))) + 1, length.out = n_new_patients),
arm = rep(c("Docetaxel", "MPDL3280A"), c(floor(avg_arm_size_followup), ceiling(avg_arm_size_followup))),
os_time = 0,
os_event = FALSE,
lost_to_follow_up = FALSE,
ecog = sample(os_data$ecog, n_new_patients, replace = TRUE),
age = sample(os_data$age, n_new_patients, replace = TRUE),
race = sample(os_data$race, n_new_patients, replace = TRUE),
sex = sample(os_data$sex, n_new_patients, replace = TRUE)
)
os_data_augmented <- os_data[, names(os_data_new)] |>
mutate(id = as.character(id)) |>
rbind(os_data_new) |>
mutate(id = factor(id))
n_censored <- sum(!os_data_augmented$os_event & !os_data_augmented$lost_to_follow_up)
n_censored
```
So now we have `r n_lost_to_follow_up` patients who have been lost to follow-up and `r n_censored` patients who are still being followed up for OS (or who will still be entering the trial). These `r n_censored` patients will be the ones we will perform the individual sampling for.
### Refit the joint model with augmented data
First we need to refit the joint model to this augmented data set. That is the easiest way to also get survival curve samples for the patients who are yet to be enrolled in the trial.
We notice that here we also need to add at least some random baseline samples to the longitudinal data set, otherwise it does not work.
```{r}
#| label: refit_joint_model_augmented
subj_aug_df <- os_data_augmented |>
mutate(study = "OAK") |>
select(study, id, arm)
subj_aug_data <- DataSubject(
data = subj_aug_df,
subject = "id",
arm = "arm",
study = "study"
)
long_df <- tumor_data |>
select(id, year, sld)
new_long_df <- os_data_new |>
select(id, os_time) |>
rename(year = os_time) |>
mutate(sld = sample(tumor_data$sld, n_new_patients, replace = TRUE))
long_aug_df <- long_df |>
mutate(id = as.character(id)) |>
rbind(new_long_df) |>
mutate(id = factor(id))
stopifnot(identical(levels(long_aug_df$id), levels(subj_aug_df$id)))
long_aug_data <- DataLongitudinal(
data = long_aug_df,
formula = sld ~ year
)
surv_aug_data <- DataSurvival(
data = os_data_augmented,
formula = Surv(os_time, os_event) ~ ecog + age + race + sex
)
joint_aug_data <- DataJoint(
subject = subj_aug_data,
longitudinal = long_aug_data,
survival = surv_aug_data
)
save_file <- here("session-pts/jm2.rds")
if (file.exists(save_file)) {
joint_aug_results <- readRDS(save_file)
} else {
joint_aug_results <- sampleStanModel(
joint_mod,
data = joint_aug_data,
iter_sampling = ITER,
iter_warmup = WARMUP,
chains = CHAINS,
parallel_chains = CHAINS,
thin = CHAINS,
seed = BAYES.SEED,
refresh = REFRESH
)
saveObject(joint_aug_results, file = save_file)
}
```
### Individual Sampling of OS events
Now we can perform the individual sampling of the OS events for the patients who are still being followed up.
Let's start with a single patient:
```{r}
#| label: individual_sampling_single_patient
patient_id <- os_data_augmented |>
filter(!os_event & !lost_to_follow_up) |>
pull(id) |>
unique() |>
head(1)
```
So for this patient `r patient_id`, we can extract the individual survival distribution MCMC samples from the joint model results along a time grid that extrapolates long enough into the future, say 10 years after the last observed OS time:
```{r}
#| label: extract_individual_survival_samples
#| cache.lazy: false
#| output: false
length_time_grid <- 100
time_grid_end <- round(max(os_data_augmented$os_time) + 10, 1)
time_grid <- seq(0, time_grid_end, length = length_time_grid)
save_file <- here("session-pts/jm2_surv_samples.rds")
if (file.exists(save_file)) {
os_surv_samples <- readRDS(save_file)
} else {
os_surv_samples <- SurvivalQuantities(
object = joint_aug_results,
grid = GridFixed(times = time_grid),
type = "surv"
)
saveRDS(os_surv_samples, file = save_file)
}
os_surv_samples_df <- as.data.frame(os_surv_samples)
os_surv_samples_patient <- os_surv_samples_df |>
filter(group == patient_id) |>
select(-group) |>
mutate(sample_id = rep(1:ITER, length_time_grid))
head(os_surv_samples_patient)
```
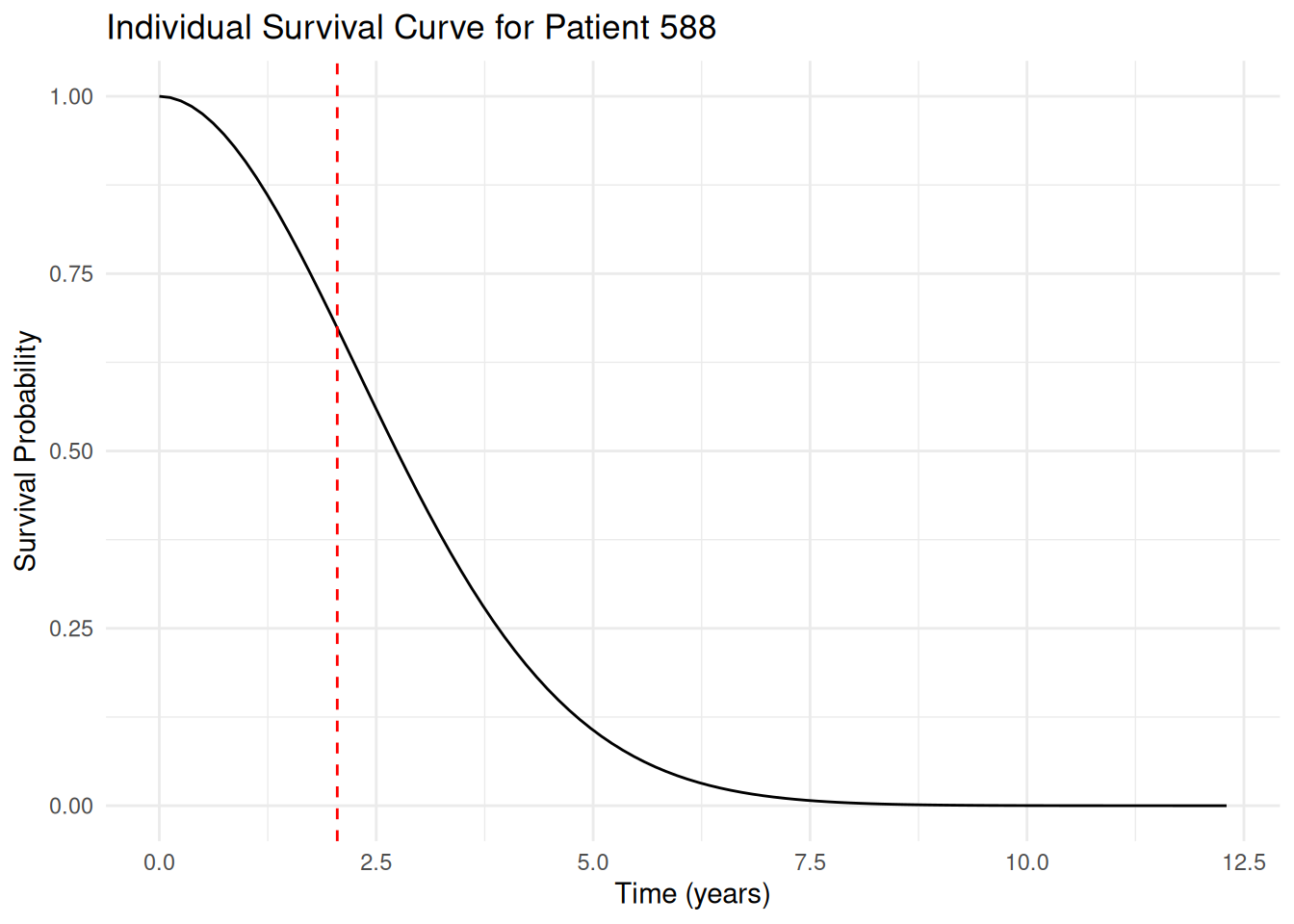
Now let's zoom in on the first sampled survival curve of this patient, where we show also the last observed OS time as a vertical dashed line:
```{r}
#| label: plot_individual_survival_curve
first_surv_sample <- os_surv_samples_patient |>
filter(sample_id == 1)
patient_last_os_time <- os_data_augmented$os_time[os_data_augmented$id == patient_id]
first_surv_sample_plot <- ggplot(first_surv_sample, aes(x = time, y = values)) +
geom_line() +
labs(
title = paste("Individual Survival Curve for Patient", patient_id),
x = "Time (years)",
y = "Survival Probability"
) +
geom_vline(
xintercept = patient_last_os_time,
linetype = "dashed",
color = "red"
) +
theme_minimal()
first_surv_sample_plot
```
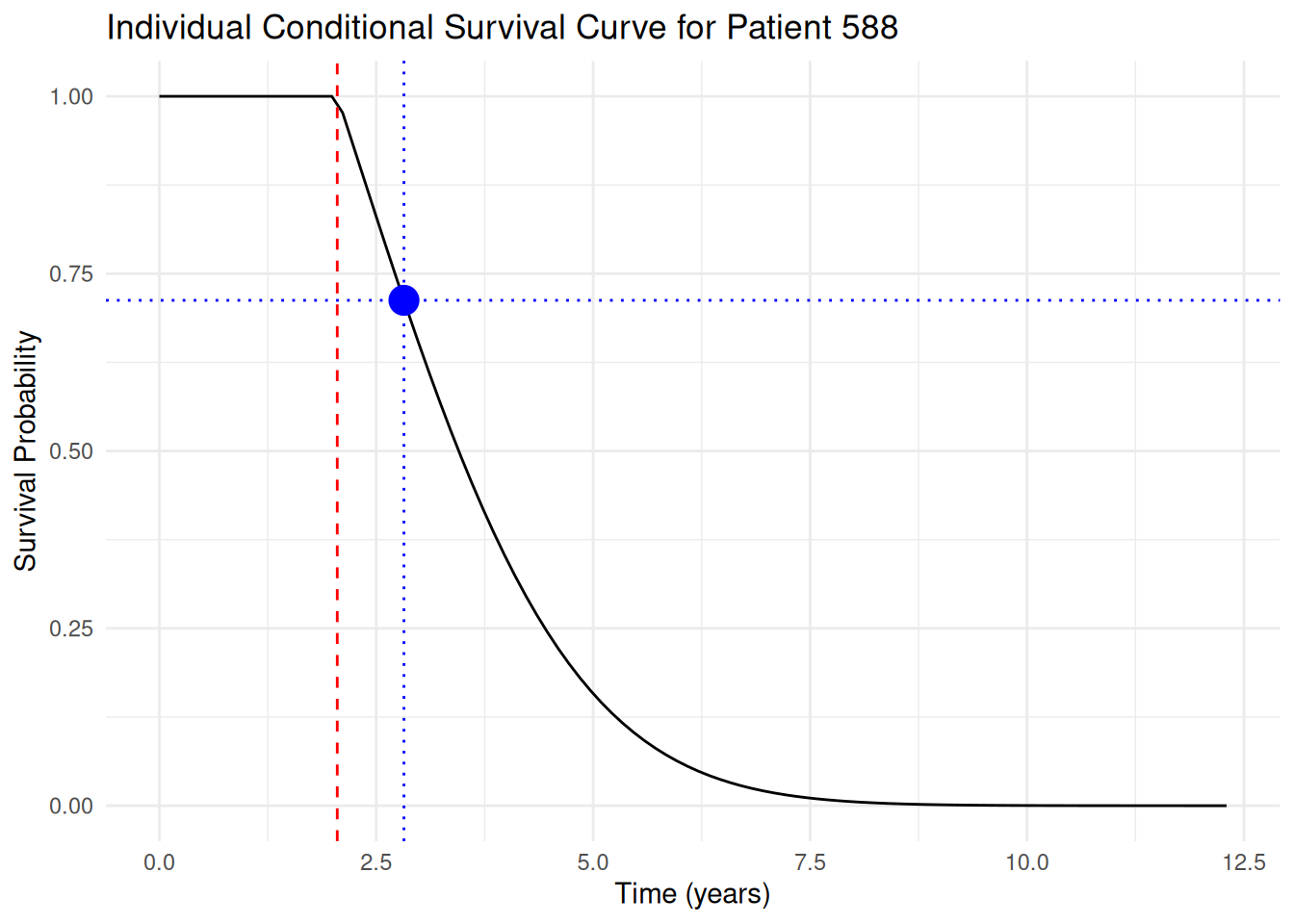
As described in the slides, we can now sample a survival time for this patient from the conditional survival distribution, given the last observed OS time, by:
1. Drawing a standard uniform random number $p \sim U(0, 1)$
1. Finding the time $t$ such that $(1-p)S(c) - S(t) = 0$ where $c = `r round(patient_last_os_time, 1)` is the last observed OS time
```{r}
#| label: sample_conditional_survival_time
set.seed(123)
p <- runif(1)
# Linear approximation function for the survival function:
surv_approx <- approxfun(
x = first_surv_sample$time,
y = first_surv_sample$values,
rule = 2 # extrapolation outside interval via closest data extreme
)
# Survival function value at the time of censoring:
surv_at_censoring <- surv_approx(patient_last_os_time)
# Find the time t such that (1-p) * S(c) - S(t) = 0:
t <- uniroot(
function(t) (1 - p) * surv_at_censoring - surv_approx(t),
interval = c(0, time_grid_end)
)$root
t
```
We can plot the conditional survival function together with this sampled survival time:
```{r}
first_surv_sample <- first_surv_sample |>
mutate(
cond_values = ifelse(
time <= patient_last_os_time,
1,
values / surv_at_censoring
)
)
first_cond_surv_sample_plot <- ggplot(
first_surv_sample,
aes(x = time, y = cond_values)
) +
geom_line() +
labs(
title = paste(
"Individual Conditional Survival Curve for Patient",
patient_id
),
x = "Time (years)",
y = "Survival Probability"
) +
geom_vline(
xintercept = patient_last_os_time,
linetype = "dashed",
color = "red"
) +
theme_minimal() +
geom_vline(
xintercept = t,
linetype = "dotted",
color = "blue"
) +
geom_hline(
yintercept = 1 - p,
linetype = "dotted",
color = "blue"
) +
geom_point(
data = data.frame(t = t, p = p),
aes(x = t, y = 1 - p),
color = "blue",
size = 5
)
first_cond_surv_sample_plot
```
The challenge is now to do this efficiently for all patients who are still being followed up for OS, and for all of their MCMC samples.
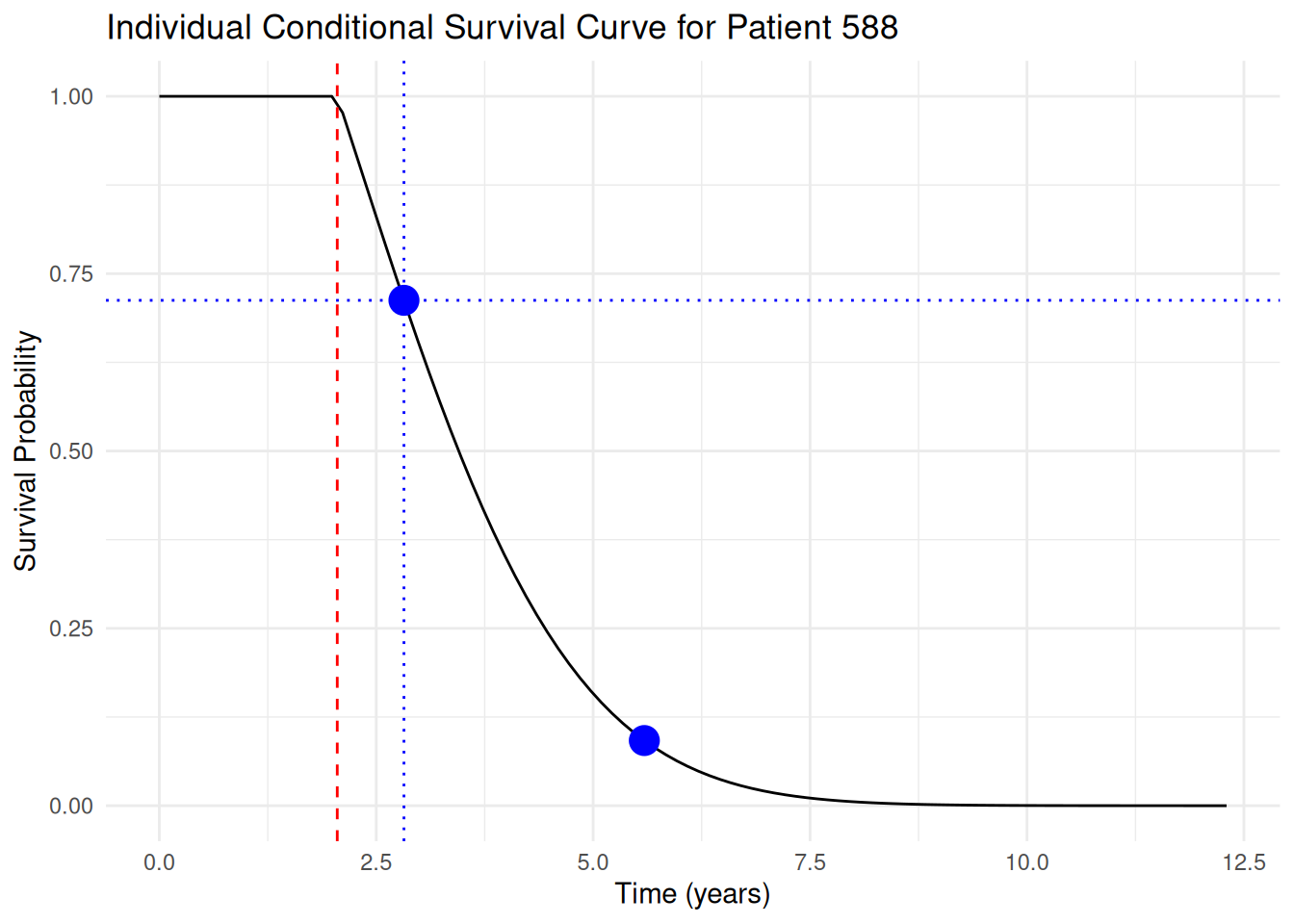
### Simplified Rcpp implementation for single patient/sample
For now, let's create a simpler `Rcpp` function that handles a single patient's single MCMC sample:
```{r}
#| label: simple_rcpp_conditional_sampling
library(Rcpp)
# Use Rcpp function for single patient, single sample.
sourceCpp(here("session-pts/conditional_sampling.cpp"))
# Test the function with a simple example.
set.seed(3453)
t_cpp_simple <- sample_single_conditional_survival_time(
time_grid = first_surv_sample$time,
surv_values = first_surv_sample$values,
censoring_time = patient_last_os_time
)
first_cond_surv_sample_plot +
geom_point(
data = data.frame(
t = t_cpp_simple$t_result,
p = t_cpp_simple$uniform_sample
),
aes(x = t, y = 1 - p),
color = "blue",
size = 5
)
```
### Rcpp implementation for all patients and samples
Let's use the second `Rcpp` function that handles all patients and all MCMC samples at once.
We just need to prepare the data in the right format:
- The first argument is the time grid, which we already have.
- The second argument is a matrix of survival values, where each row is a sample/patient combination and each column is a time point.
- The third argument is a vector of censoring times, where each element corresponds to a sample/patient combination.
```{r}
#| label: rcpp_conditional_sampling_all
# First subset to the patients where we need to sample from the conditional survival distribution.
pt_to_sample <- os_data_augmented |>
filter(!os_event & !lost_to_follow_up)
pt_to_sample_ids <- pt_to_sample$id
qs <- os_surv_samples@quantities
include_qs <- qs@groups %in% pt_to_sample_ids
qs_samples <- qs@quantities[, include_qs]
qs_times <- qs@times[include_qs]
qs_groups <- qs@groups[include_qs]
surv_values_samples <- matrix(
qs_samples,
nrow = ITER * length(pt_to_sample_ids),
ncol = length_time_grid
)
dim(surv_values_samples)
surv_values_pt_ids <- rep(
head(qs_groups, length(pt_to_sample_ids)),
each = ITER
)
censoring_times <- pt_to_sample$os_time[match(
surv_values_pt_ids,
pt_to_sample_ids
)]
length(censoring_times)
cond_surv_time_samples <- sample_conditional_survival_times(
time_grid = time_grid,
surv_values = surv_values_samples,
censoring_times = censoring_times
)
mean(cond_surv_time_samples$beyond_max_time)
summary(cond_surv_time_samples$t_results)
hist(cond_surv_time_samples$uniform_samples)
os_cond_samples <- matrix(
cond_surv_time_samples$t_results,
nrow = ITER,
ncol = length(pt_to_sample_ids),
dimnames = list(seq_len(ITER), head(qs_groups, length(pt_to_sample_ids)))
)
```
So this function is very fast, and in this case we have less than 1% of the samples where we did not have a long enough time grid, which seems sufficient for our purposes.
### Generating OS data set samples
Now that we have the OS events for the patients who are still being followed up, we can generate the complete OS data set samples for each MCMC sample.
```{r}
#| label: generate_os_data_samples
# Where do we need to replace the OS times?
os_rows_to_replace <- match(
pt_to_sample_ids,
os_data_augmented$id
)
# From which column do we take the sampled OS times?
os_cond_samples_cols <- match(
pt_to_sample_ids,
colnames(os_cond_samples)
)
os_data_samples <- lapply(1:ITER, function(i) {
# Create a copy of the original OS data
os_data_sample <- os_data_augmented[, c("id", "arm", "os_time", "os_event", "race", "sex", "ecog", "age")]
# Add the sampled OS times for the patients who are still being followed up.
os_data_sample$os_time[os_rows_to_replace] <- os_cond_samples[
i,
os_cond_samples_cols
]
# Set the OS event to TRUE for those patients, because we assume they have an event now.
os_data_sample$os_event[os_rows_to_replace] <- TRUE
os_data_sample
})
```
### Calculate log rank statistic for each sampled OS data set
Now it is easy to calculate the log-rank test statistic for each sampled OS data set.
Here we don't adjust for any covariates.
```{r}
#| label: calculate_log_rank_statistic
log_rank_stats_fun <- function(df) {
surv_diff <- survival::survdiff(
Surv(os_time, os_event) ~ arm,
data = df
)
surv_diff$chisq
}
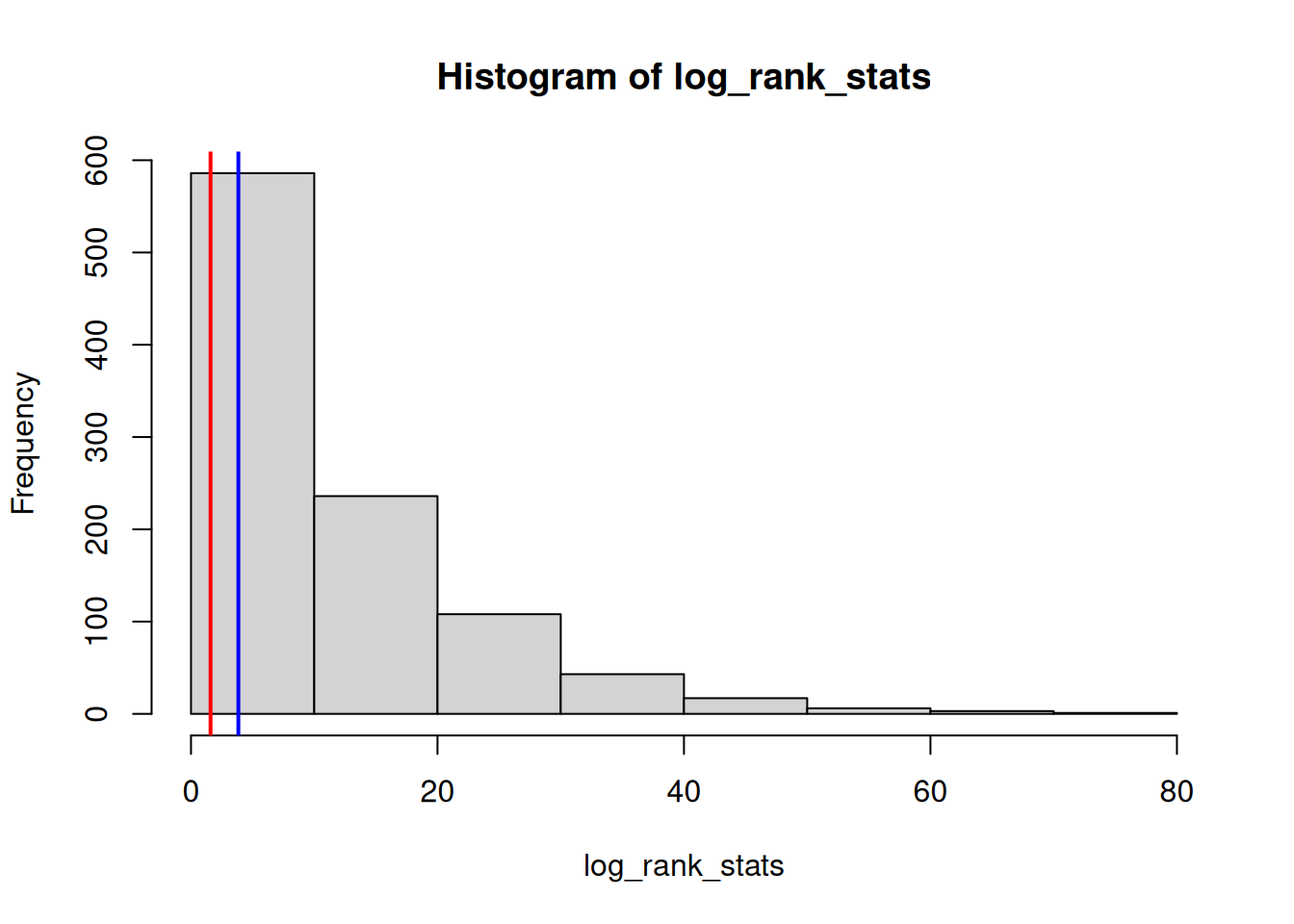
log_rank_stats <- sapply(os_data_samples, log_rank_stats_fun)
hist(log_rank_stats)
log_rank_at_ia <- log_rank_stats_fun(os_data_augmented)
log_rank_at_ia
abline(v = log_rank_at_ia, col = "red", lwd = 2)
critical_value <- qchisq(0.95, df = 1)
abline(v = critical_value, col = "blue", lwd = 2)
```
And using the critical value of the log-rank test statistic for a significance level of 0.05, we can calculate the PTS:
```{r}
#| label: calculate_pts_log_rank
pts_log_rank <- mean(log_rank_stats > critical_value)
pts_log_rank
```
So we see that this PTS with `r round(pts_log_rank * 100, 1)`% is a bit lower than the previous PTS estimates.
### Hazard Ratio based PTS
We can also calculate the PTS in an analogous way using the hazard ratio estimates:
```{r}
#| label: calculate_pts_hr
hr_pval_fun <- function(df) {
cox_mod <- survival::coxph(
Surv(os_time, os_event) ~ arm + ecog + age + race + sex,
data = df
)
summary(cox_mod)$coefficients[1, 5]
}
hr_pvals <- sapply(os_data_samples, hr_pval_fun)
pts_hr <- mean(hr_pvals < 0.05)
pts_hr
```
In this PTS estimate we can adjust for the covariates. We see that the result of `r round(pts_hr * 100, 1)`% is in line with the frequentist based PTS estimate for the HR which we calculated earlier.
### Plot Kaplan-Meier curves predictions
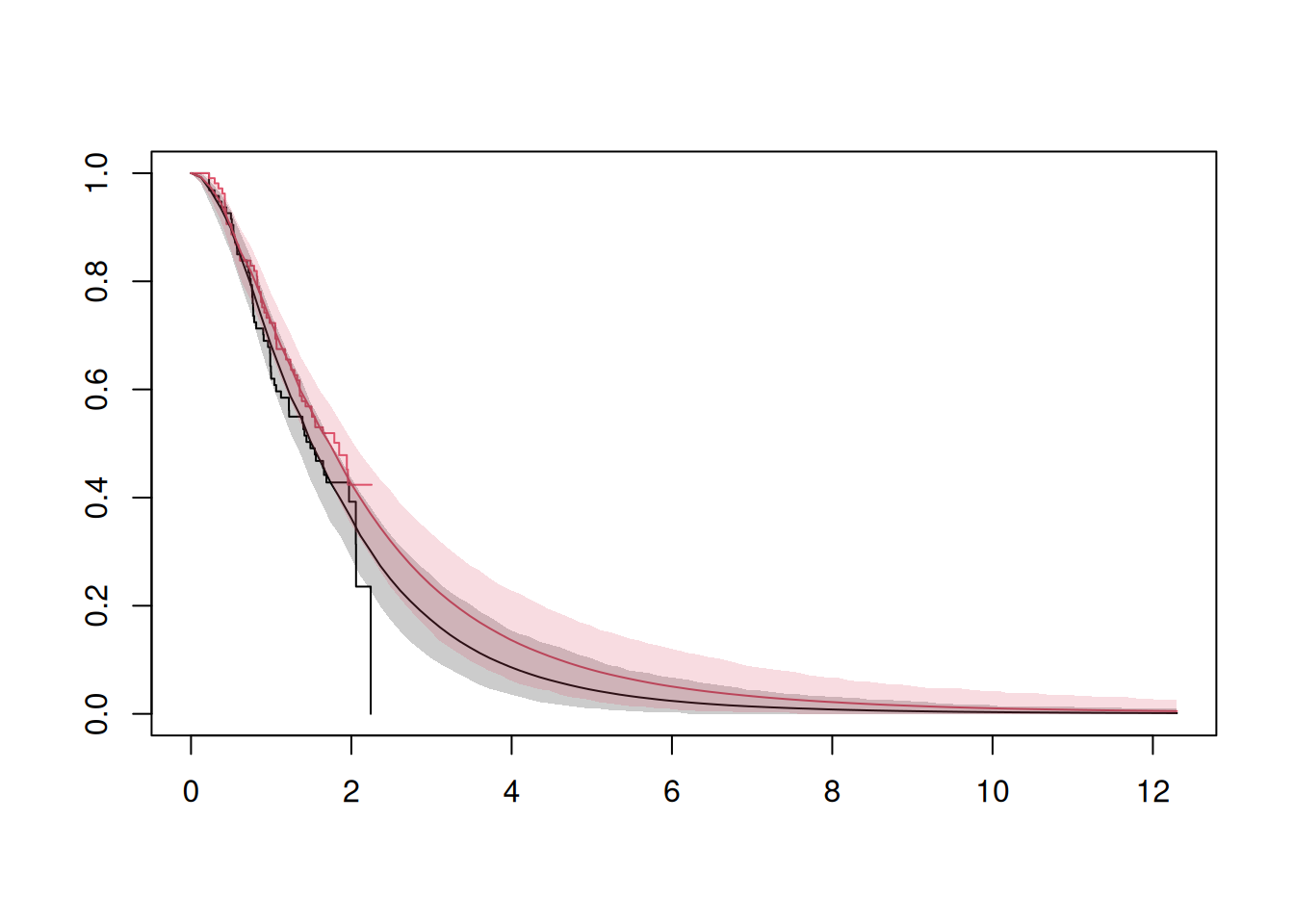
Similarly we can extract the Kaplan-Meier curves for each sampled OS data set and plot them:
```{r}
#| label: plot_kaplan_meier_curves
km_curves <- lapply(os_data_samples, function(df) {
survfit_obj <- survival::survfit(Surv(os_time, os_event) ~ arm, data = df)
times <- survfit_obj$time
surv_probs <- survfit_obj$surv
strata <- survfit_obj$strata
n_control <- strata[1]
n_treatment <- strata[2]
control_fun <- stepfun(
times[1:n_control],
c(1, surv_probs[1:n_control]),
right = TRUE
)
treatment_fun <- stepfun(
times[(n_control + 1):length(times)],
c(1, surv_probs[(n_control + 1):length(surv_probs)]),
right = TRUE
)
control_vals <- control_fun(time_grid)
treatment_vals <- treatment_fun(time_grid)
list(control = control_vals, treatment = treatment_vals)
})
km_control_samples <- sapply(km_curves, function(x) x$control)
km_treatment_samples <- sapply(km_curves, function(x) x$treatment)
survfit_ia <- survival::survfit(Surv(os_time, os_event) ~ arm, data = os_data_augmented)
plot(survfit_ia, col = c(1, 2), xlim = c(0, max(time_grid)))
# Add the mean KM curves for each arm.
lines(time_grid, rowMeans(km_control_samples), col = 1)
lines(time_grid, rowMeans(km_treatment_samples), col = 2)
# Add pointwise confidence intervals as shaded areas.
km_control_ci <- apply(km_control_samples, 1, quantile, probs = c(0.025, 0.975))
km_treatment_ci <- apply(
km_treatment_samples,
1,
quantile,
probs = c(0.025, 0.975)
)
polygon(
c(time_grid, rev(time_grid)),
c(km_control_ci[1, ], rev(km_control_ci[2, ])),
col = adjustcolor(1, alpha.f = 0.2),
border = NA
)
polygon(
c(time_grid, rev(time_grid)),
c(km_treatment_ci[1, ], rev(km_treatment_ci[2, ])),
col = adjustcolor(2, alpha.f = 0.2),
border = NA
)
```
We can see that we assume a very long follow up of the data here.
Obviously we could cut the data sets at a certain number of events or a specific time point easily.