---
title: "2. TGI model minimal workflow with `jmpost`"
author:
- Daniel Sabanés Bové
- Francois Mercier
date: last-modified
editor_options:
chunk_output_type: inline
format:
html:
code-fold: show
html-math-method: mathjax
cache: true
---
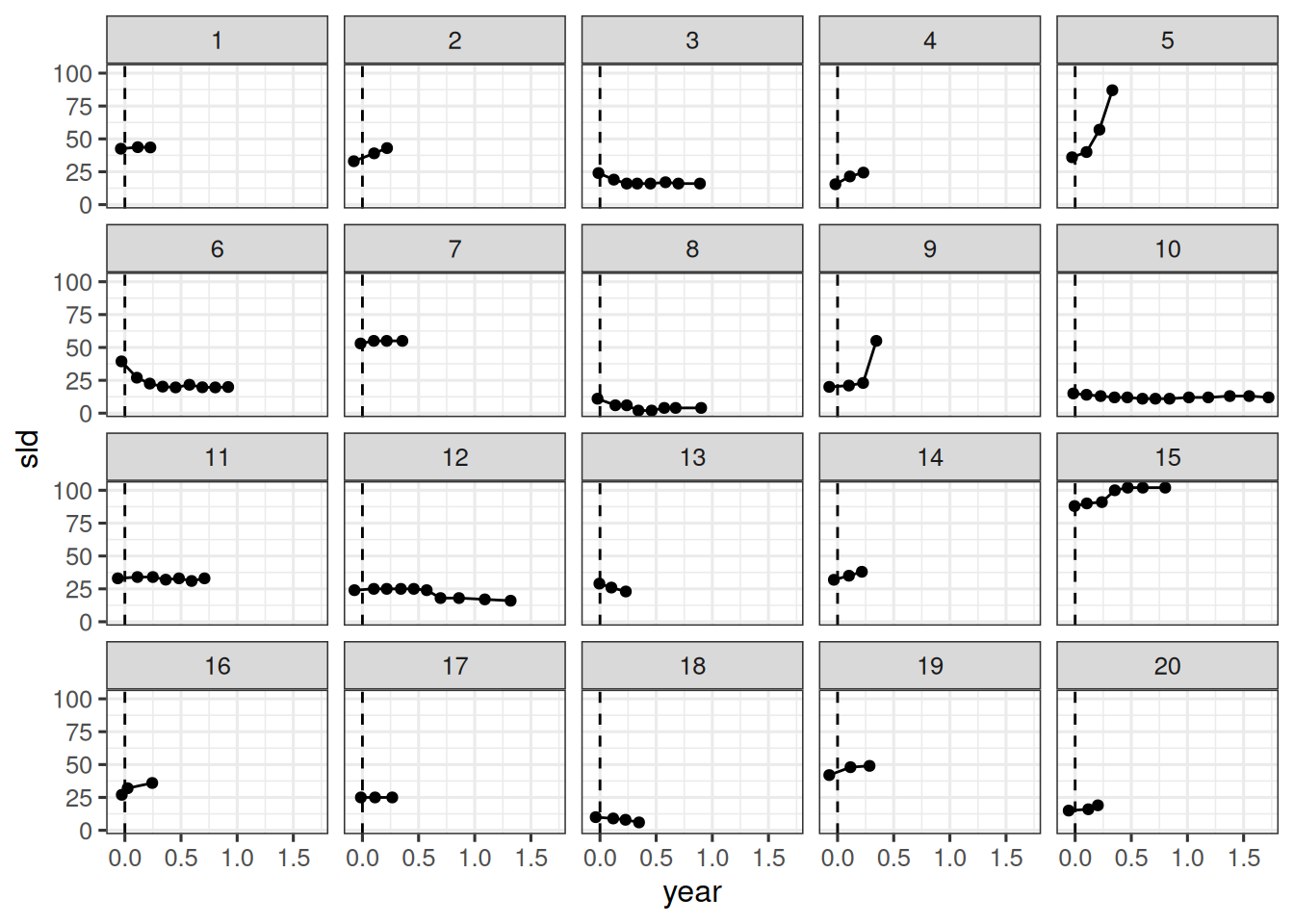
Let's try to fit the same model now with `jmpost`. We will use the same data as in the previous notebook.
## Setup and load data
{{< include _setup_and_load.qmd >}}
{{< include _load_data.qmd >}}
## Data preparation
We start with the subject level data set.
For the beginning, we want to treat all observations as if they come from a single arm and single study for now. Therefore we insert constant study and arm values here.
```{r}
#| label: subj_df_prep
subj_df <- data.frame(
id = unique(df$id),
arm = "arm",
study = "study"
)
subj_data <- DataSubject(
data = subj_df,
subject = "id",
arm = "arm",
study = "study"
)
```
Next we prepare the longitudinal data object.
```{r}
#| label: long_df_prep
long_df <- df |>
select(id, year, sld)
long_data <- DataLongitudinal(
data = long_df,
formula = sld ~ year
)
```
Now we can create the `JointData` object:
```{r}
#| label: joint_data_prep
joint_data <- DataJoint(
subject = subj_data,
longitudinal = long_data
)
```
## Model specification
The statistical model is specified in the `jmpost` vignette [here](https://genentech.github.io/jmpost/main/articles/statistical-specification.html#stein-fojo-model).
Here we just want to fit the longitudinal data, therefore:
```{r}
#| label: tgi_mod_spec
tgi_mod <- JointModel(
longitudinal = LongitudinalSteinFojo(
mu_bsld = prior_normal(log(65), 1),
mu_ks = prior_normal(log(0.52), 1),
mu_kg = prior_normal(log(1.04), 1),
omega_bsld = prior_normal(0, 3) |> set_limits(0, Inf),
omega_ks = prior_normal(0, 3) |> set_limits(0, Inf),
omega_kg = prior_normal(0, 3) |> set_limits(0, Inf),
sigma = prior_normal(0, 3) |> set_limits(0, Inf)
)
)
```
Note that the priors on the standard deviations, `omega_*` and `sigma`, are truncated to the positive domain. So we used here truncated normal priors.
## Fit model
We can now fit the model using `jmpost`.
```{r}
#| label: fit_model
save_file <- here("session-tgi/jm5.RData")
if (file.exists(save_file)) {
load(save_file)
} else {
mcmc_results <- sampleStanModel(
tgi_mod,
data = joint_data,
iter_sampling = ITER,
iter_warmup = WARMUP,
chains = CHAINS,
parallel_chains = CHAINS,
thin = CHAINS,
seed = BAYES.SEED,
refresh = REFRESH
)
save(mcmc_results, file = save_file)
}
```
Let's check the convergence of the population parameters:
```{r}
#| label: check_convergence
#| dependson: fit_model
vars <- c(
"lm_sf_mu_bsld",
"lm_sf_mu_ks",
"lm_sf_mu_kg",
"lm_sf_sigma",
"lm_sf_omega_bsld",
"lm_sf_omega_ks",
"lm_sf_omega_kg"
)
save_overall_file <- here("session-tgi/jm5_more.RData")
if (file.exists(save_overall_file)) {
load(save_overall_file)
} else {
mcmc_res_cmdstan <- cmdstanr::as.CmdStanMCMC(mcmc_results)
mcmc_res_sum <- mcmc_res_cmdstan$summary(vars)
vars_draws <- mcmc_res_cmdstan$draws(vars)
loo_res <- mcmc_res_cmdstan$loo(r_eff = FALSE)
save(mcmc_res_sum, vars_draws, loo_res, file = save_overall_file)
}
mcmc_res_sum
```
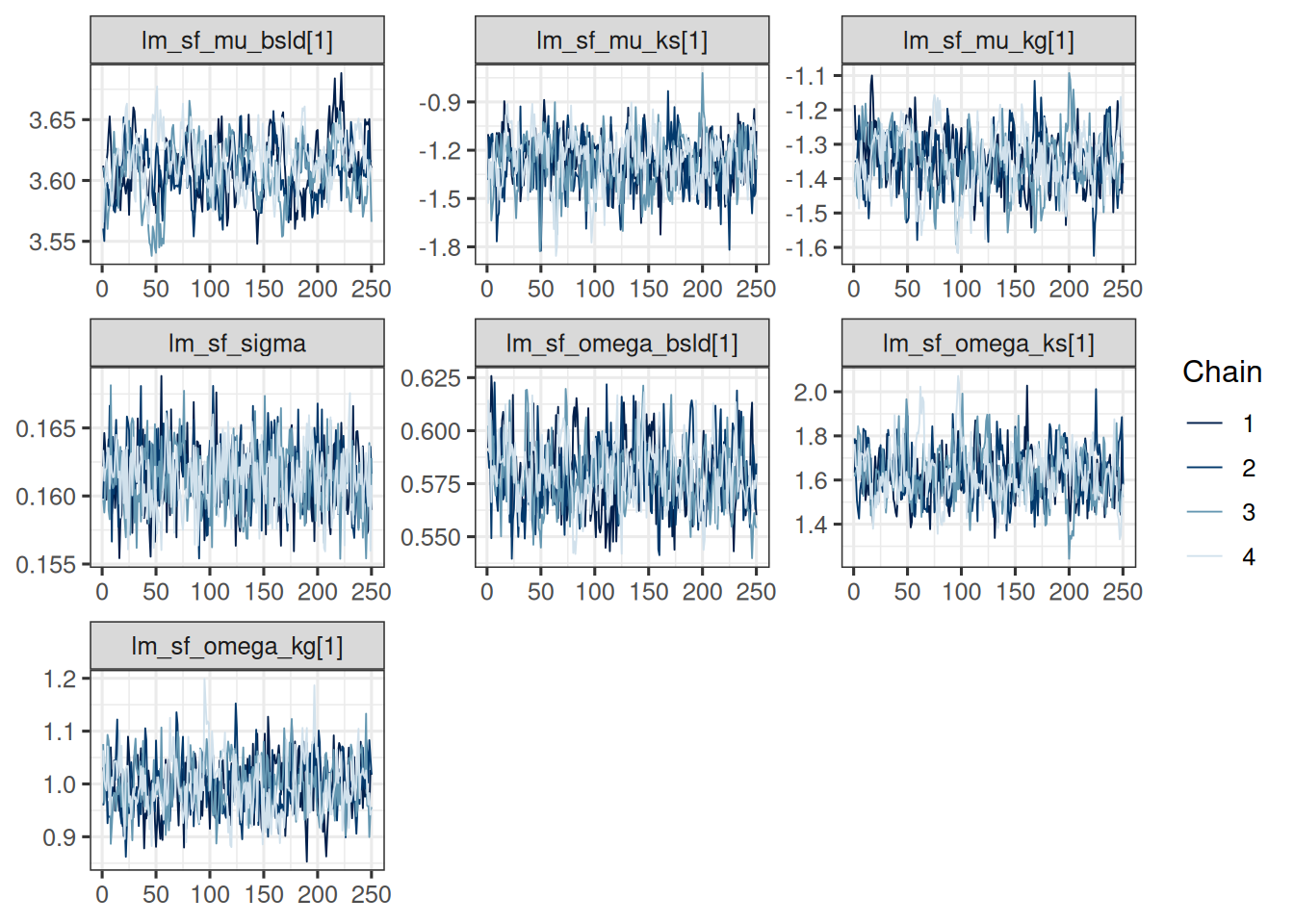
This looks good, let's check the traceplots:
```{r}
#| label: plot_trace
#| dependson: check_convergence
# vars_draws <- mcmc_res_cmdstan$draws(vars)
mcmc_trace(vars_draws)
```
They also look ok, all chains are mixing well in the same range of parameter values.
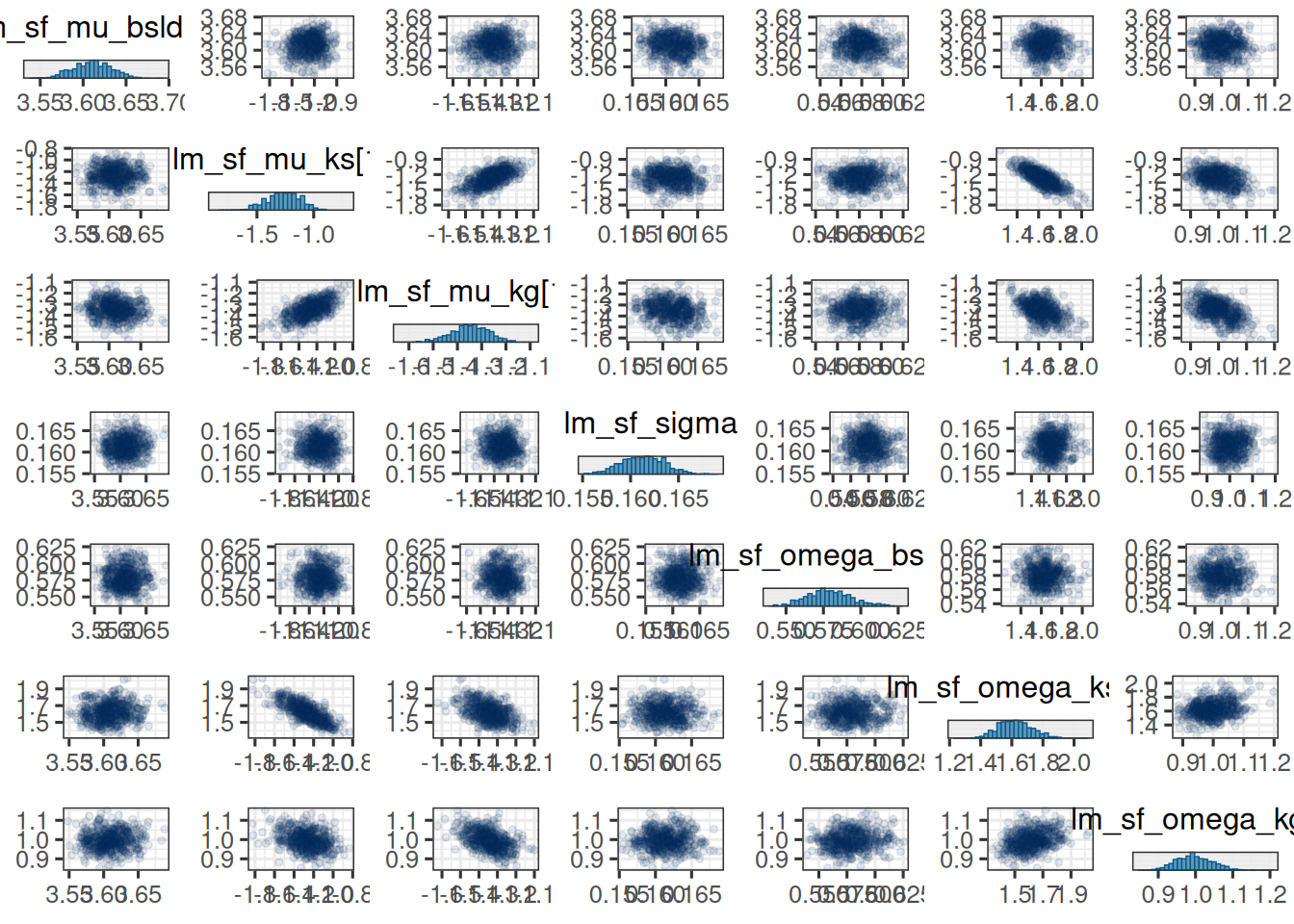
Also here we could look at the pairs plot:
```{r}
#| label: plot_pairs
mcmc_pairs(
vars_draws,
off_diag_args = list(size = 1, alpha = 0.1)
)
```
## Observation vs. model fit
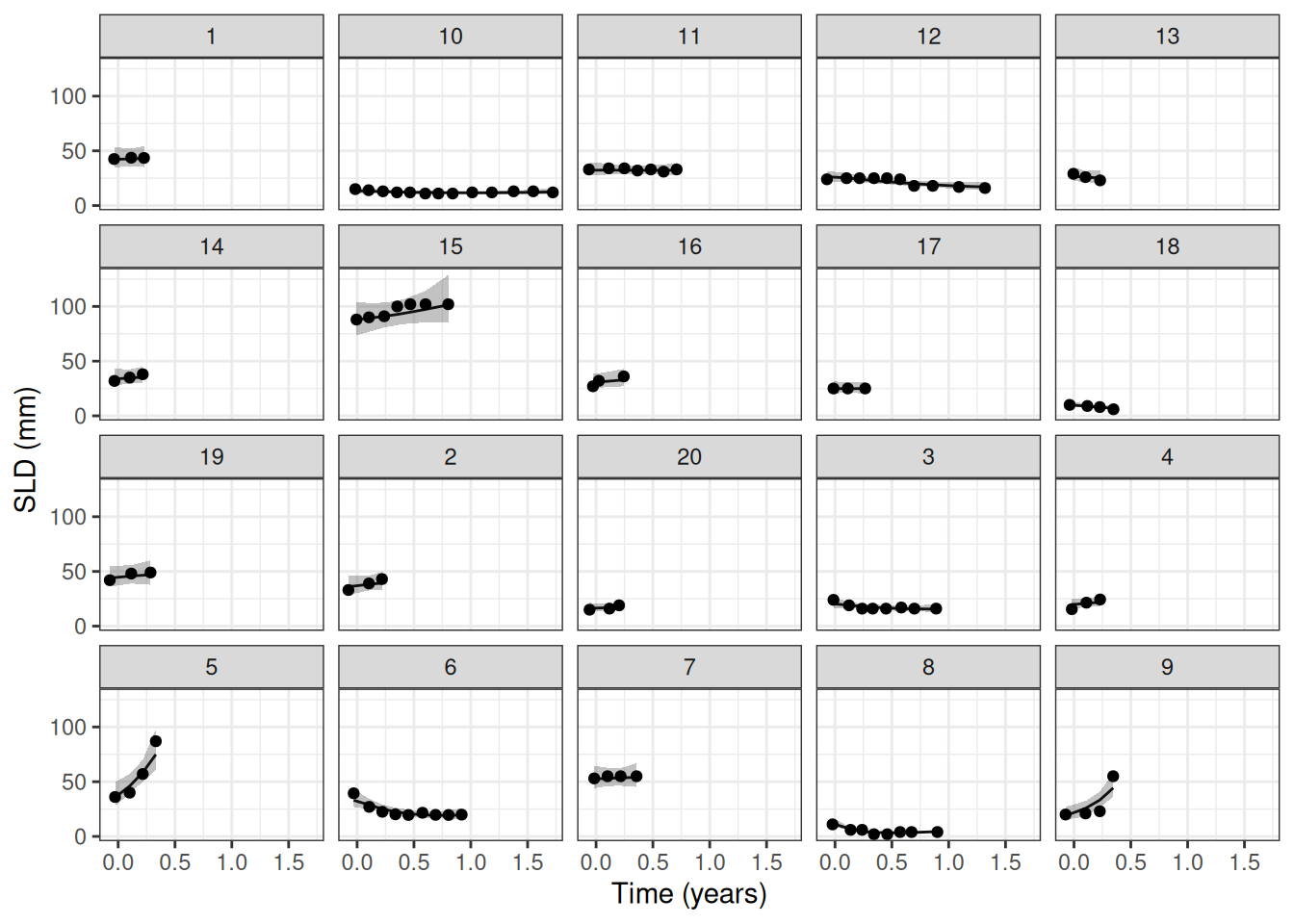
Let's check the fit of the model to the data:
```{r}
#| label: plot_fit
#| dependson: fit_model
pt_subset <- as.character(1:20)
save_fit_file <- here("session-tgi/jm5_fit.RData")
if (file.exists(save_fit_file)) {
load(save_fit_file)
} else {
fit_subset <- LongitudinalQuantities(
mcmc_results,
grid = GridObserved(subjects = pt_subset)
)
save(fit_subset, file = save_fit_file)
}
autoplot(fit_subset)+
labs(x = "Time (years)", y = "SLD (mm)")
```
So this works very nicely.
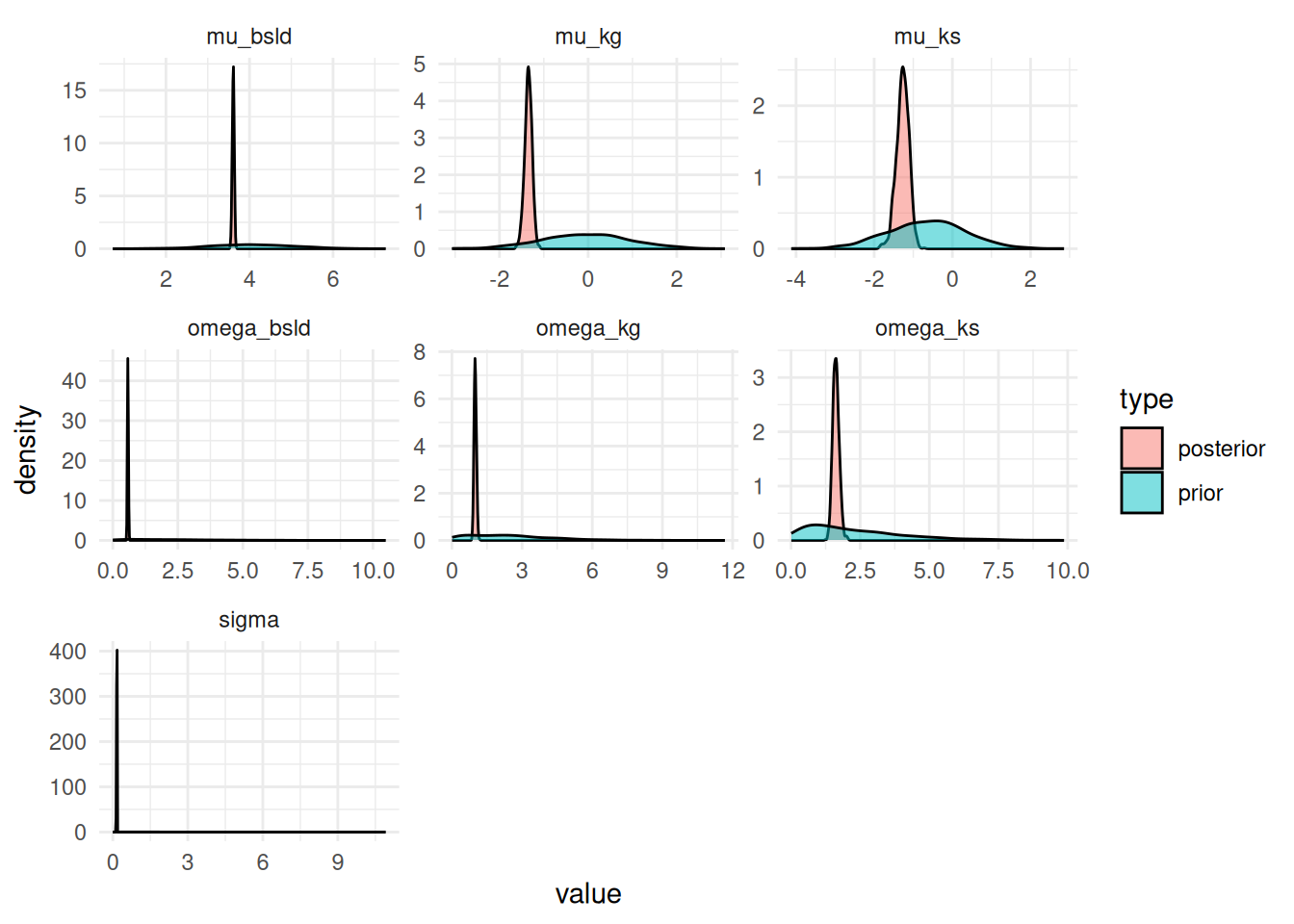
## Prior vs. posterior
Let's check the prior vs. posterior for the parameters:
```{r}
#| label: plot_prior_post
#| dependson: plot_trace
post_samples <- as_draws_df(vars_draws) |>
rename(
mu_bsld = "lm_sf_mu_bsld[1]",
mu_ks = "lm_sf_mu_ks[1]",
mu_kg = "lm_sf_mu_kg[1]",
omega_bsld = "lm_sf_omega_bsld[1]",
omega_ks = "lm_sf_omega_ks[1]",
omega_kg = "lm_sf_omega_kg[1]",
sigma = lm_sf_sigma
) |>
mutate(type = "posterior") |>
select(mu_bsld, mu_ks, mu_kg, omega_bsld, omega_ks, omega_kg, sigma, type)
n_prior_samples <- nrow(post_samples)
prior_samples <- data.frame(
mu_bsld = rnorm(n_prior_samples, log(65), 1),
mu_ks = rnorm(n_prior_samples, log(0.52), 1),
mu_kg = rnorm(n_prior_samples, log(1.04), 1),
omega_bsld = rtruncnorm(n_prior_samples, a = 0, mean = 0, sd = 3),
omega_ks = rtruncnorm(n_prior_samples, a = 0, mean = 0, sd = 3),
omega_kg = rtruncnorm(n_prior_samples, a = 0, mean = 0, sd = 3),
sigma = rtruncnorm(n_prior_samples, a = 0, mean = 0, sd = 3)
) |>
mutate(type = "prior")
# Combine the two
combined_samples <- rbind(post_samples, prior_samples) |>
pivot_longer(cols = -type, names_to = "parameter", values_to = "value")
ggplot(combined_samples, aes(x = value, fill = type)) +
geom_density(alpha = 0.5) +
facet_wrap(~parameter, scales = "free") +
theme_minimal()
```
This looks good, because the priors are covering the range of the posterior samples and are not too informative.
## Parameter estimates
Here we need again to be careful: We are interested in the posterior mean estimates of the baseline, shrinkage and growth population rates on the original scale. Because we model them on the log scale as normal distributed, we need to use the mean of the log-normal distribution to get the mean on the original scale.
```{r}
#| label: par_estimates
#| dependson: plot_prior_post
post_sum <- post_samples |>
mutate(
theta_b0 = exp(mu_bsld + omega_bsld^2 / 2),
theta_ks = exp(mu_ks + omega_ks^2 / 2),
theta_kg = exp(mu_kg + omega_kg^2 / 2),
cv_0 = sqrt(exp(omega_bsld^2) - 1),
cv_s = sqrt(exp(omega_ks^2) - 1),
cv_g = sqrt(exp(omega_kg^2) - 1)
) |>
select(theta_b0, theta_ks, theta_kg, omega_bsld, omega_ks, omega_kg, cv_0, cv_s, cv_g, sigma) |>
summarize_draws() |>
gt() |>
fmt_number(n_sigfig = 3)
post_sum
```
We can see that these are consistent with the estimates from the `brms` model earlier.
## Separate arm estimates
While there is no general covariates support in `jmpost` for the longitudinal models as of now, we can obtain separate estimates for the longitudinal model parameters: As detailed in the model specification [here](https://genentech.github.io/jmpost/main/articles/statistical-specification.html#stein-fojo-model), as soon as we have the arm defined, then separate estimates for the arm-specific shrinkage and growth parameters will be obtained: Both the population means and standard deviation parameters are here arm-specific. (Note that this is slightly different from `brms` where we assumed earlier the same standard deviation independent of the treatment arm.)
So we need to define the subject data accordingly now with the arm information:
```{r}
#| label: subj_df_prep_arm
subj_df_by_arm <- df |>
select(id, arm) |>
distinct() |>
mutate(study = "study")
subj_data_by_arm <- DataSubject(
data = subj_df_by_arm,
subject = "id",
arm = "arm",
study = "study"
)
```
We redefine the `JointData` object and can then fit the model, because the prior specification does not need to change: We assume iid priors on the arm-specific parameters here.
```{r}
#| label: joint_data_prep_arm
joint_data_by_arm <- DataJoint(
subject = subj_data_by_arm,
longitudinal = long_data
)
```
```{r}
#| label: fit_model_arm
save_file <- here("session-tgi/jm6.RData")
if (file.exists(save_file)) {
load(save_file)
} else {
mcmc_results_by_arm <- sampleStanModel(
tgi_mod,
data = joint_data_by_arm,
iter_sampling = ITER,
iter_warmup = WARMUP,
chains = CHAINS,
parallel_chains = CHAINS,
thin = CHAINS,
seed = BAYES.SEED,
refresh = REFRESH
)
save(mcmc_results_by_arm, file = save_file)
}
```
Let's again check the convergence:
```{r}
#| label: check_convergence_arm
#| dependson: fit_model_arm
vars <- c(
"lm_sf_mu_bsld",
"lm_sf_mu_ks",
"lm_sf_mu_kg",
"lm_sf_sigma",
"lm_sf_omega_bsld",
"lm_sf_omega_ks",
"lm_sf_omega_kg"
)
save_arm_file <- here("session-tgi/jm6_more.RData")
if (file.exists(save_arm_file)) {
load(save_arm_file)
} else {
mcmc_res_cmdstan_by_arm <- cmdstanr::as.CmdStanMCMC(mcmc_results_by_arm)
mcmc_res_sum_by_arm <- mcmc_res_cmdstan_by_arm$summary(vars)
vars_draws_by_arm <- mcmc_res_cmdstan_by_arm$draws(vars)
loo_by_arm <- mcmc_res_cmdstan_by_arm$loo(r_eff = FALSE)
save(mcmc_res_sum_by_arm, vars_draws_by_arm, loo_by_arm, file = save_arm_file)
}
mcmc_res_sum_by_arm
```
Let's again tabulate the parameter estimates:
```{r}
#| label: par_estimates_arm
#| dependson: check_convergence_arm
post_samples_by_arm <- as_draws_df(vars_draws_by_arm) |>
rename(
mu_bsld = "lm_sf_mu_bsld[1]",
mu_ks1 = "lm_sf_mu_ks[1]",
mu_ks2 = "lm_sf_mu_ks[2]",
mu_kg1 = "lm_sf_mu_kg[1]",
mu_kg2 = "lm_sf_mu_kg[2]",
omega_bsld = "lm_sf_omega_bsld[1]",
omega_ks1 = "lm_sf_omega_ks[1]",
omega_ks2 = "lm_sf_omega_ks[2]",
omega_kg1 = "lm_sf_omega_kg[1]",
omega_kg2 = "lm_sf_omega_kg[2]",
sigma = lm_sf_sigma
) |>
mutate(
theta_b0 = exp(mu_bsld + omega_bsld^2 / 2),
theta_ks1 = exp(mu_ks1 + omega_ks1^2 / 2),
theta_ks2 = exp(mu_ks2 + omega_ks2^2 / 2),
theta_kg1 = exp(mu_kg1 + omega_kg1^2 / 2),
theta_kg2 = exp(mu_kg2 + omega_kg2^2 / 2),
cv_0 = sqrt(exp(omega_bsld^2) - 1),
cv_s1 = sqrt(exp(omega_ks1^2) - 1),
cv_s2 = sqrt(exp(omega_ks2^2) - 1),
cv_g1 = sqrt(exp(omega_kg1^2) - 1),
cv_g2 = sqrt(exp(omega_kg2^2) - 1)
)
post_sum_by_arm <- post_samples_by_arm |>
select(
theta_b0, theta_ks1, theta_ks2, theta_kg1, theta_kg2,
omega_bsld, omega_ks1, omega_ks2, omega_kg1, omega_kg2,
cv_0, cv_s1, cv_s2, cv_g1, cv_g2, sigma) |>
summarize_draws() |>
gt() |>
fmt_number(n_sigfig = 3)
post_sum_by_arm
```
Here again the shrinkage rate in the treatment arm 1 seems higher than in the treatment arm 2. However, the difference is not as pronounced as in the `brms` model before with the same standard deviation for both arms. We can again calculate the posterior probability that the shrinkage rate in arm 1 is higher than in arm 2:
```{r}
prob_ks1_greater_ks2 <- mean(post_samples_by_arm$theta_ks1 > post_samples_by_arm$theta_ks2)
prob_ks1_greater_ks2
```
So the posterior probability is now only around `r round(prob_ks1_greater_ks2 * 100)`%.
## Model comparison with LOO
As we have seen for `brms`, also for `jmpost` we can easily compute the LOO criterion:
```{r}
#| label: loo
#| dependson: check_convergence
# loo_res <- mcmc_res_cmdstan$loo(r_eff = FALSE)
loo_res
```
Underneath this is using the [$loo()](https://mc-stan.org/cmdstanr/reference/fit-method-loo.html) method from `cmdstanr`.
And we can compare this to the LOO of the model with separate arm estimates:
```{r}
#| label: loo_arm
#| dependson: check_convergence_arm
# loo_by_arm <- mcmc_res_cmdstan_by_arm$loo(r_eff = FALSE)
loo_by_arm
```
So the model by treatment arm performs here better than the model without treatment arm specific growth and shrinkage parameters.
## Tipps and tricks
- Also here it is possible to look at the underlying Stan code:
```{r}
#| eval: false
#| label: show_stan_code
tmp <- tempfile(fileext = ".stan") # file extension for syntax highlighting
write_stan(tgi_mod, destination = tmp)
file.edit(tmp) # opens the Stan file in the default editor
```
- It is not trivial to transport saved models from one computer to another. This is because `cmdstanr` only loads the results it currently needs from disk into memory, and thus into the R session. If you want to transport the model to another computer, you need to save the Stan code and the data, and then re-run the model on the other computer. This is because the model object in R is only a reference to the model on disk, not the model itself. Note that there is the `$save_object()` method, see [here](https://mc-stan.org/cmdstanr/reference/fit-method-save_object.html), however this leads to very large files (here about 300 MB for one fit) and can thus not be uploaded to typical git repositories. Therefore above we saved interim result objects separately as needed.
- It is important to explicitly define the truncation boundaries for the truncated normal priors, because otherwise the MCMC results will not be correct.