---
title: "3. Generalized Stein-Fojo model"
author:
- Daniel Sabanés Bové
- Francois Mercier
date: last-modified
editor_options:
chunk_output_type: inline
format:
html:
code-fold: show
html-math-method: mathjax
cache: true
---
This appendix shows how the generalized Stein-Fojo model can be implemented in a Bayesian framework using the `brms` package in R.
## Setup and load data
{{< include _setup_and_load.qmd >}}
{{< include _load_data.qmd >}}
## Generalized Stein-Fojo model
Here we have an additional parameter $\phi$, which is the weight for the shrinkage in the double exponential model. The model is then:
$$
y^{*}(t_{ij}) = \psi_{b_{0}i} \{
\psi_{\phi i} \exp(- \psi_{k_{s}i} \cdot t_{ij}) +
(1 - \psi_{\phi i}) \exp(\psi_{k_{g}i} \cdot t_{ij})
\}
$$
for positive times $t_{ij}$. Again, if the time $t$ is negative, i.e. the treatment has not started yet, then it is reasonable to assume that the tumor cannot shrink yet. That is, we have then $\phi_i = 0$. Therefore, the final model for the mean SLD is:
$$
y^{*}(t_{ij}) =
\begin{cases}
\psi_{b_{0}i} \exp(\psi_{k_{g}i} \cdot t_{ij}) & \text{if } t_{ij} < 0 \\
\psi_{b_{0}i} \{
\psi_{\phi i} \exp(- \psi_{k_{s}i} \cdot t_{ij}) +
(1 - \psi_{\phi i}) \exp(\psi_{k_{g}i} \cdot t_{ij})
\} & \text{if } t_{ij} \geq 0
\end{cases}
$$
In terms of likelihood and priors, we can use the same assumptions as in the previous model. The only difference is that we have to model the $\phi$ parameter. We can use a logit-normal distribution for this parameter. This is a normal distribution on the logit scale, which is then transformed to the unit interval.
$$
\psi_{\phi i} \sim \text{LogitNormal}(\text{logit}(0.5) = 0, 0.5)
$$
## Fit model
We can now fit the model using `brms`. The structure is determined by the model formula:
```{r}
#| label: specify_gsf_model
formula <- bf(sld ~ ystar, nl = TRUE) +
# Define the mean for the likelihood
nlf(
ystar ~
int_step(year > 0) *
(b0 * (phi * exp(-ks * year) + (1 - phi) * exp(kg * year))) +
int_step(year <= 0) *
(b0 * exp(kg * year))
) +
# As before:
nlf(sigma ~ log(tau) + log(ystar)) +
lf(tau ~ 1) +
# Define nonlinear parameter transformations:
nlf(b0 ~ exp(lb0)) +
nlf(phi ~ inv_logit(tphi)) +
nlf(ks ~ exp(lks)) +
nlf(kg ~ exp(lkg)) +
# Define random effect structure:
lf(lb0 ~ 1 + (1 | id)) +
lf(tphi ~ 1 + (1 | id)) +
lf(lks ~ 1 + (1 | id)) +
lf(lkg ~ 1 + (1 | id))
# Define the priors
priors <- c(
prior(normal(log(65), 1), nlpar = "lb0"),
prior(normal(log(0.52), 0.1), nlpar = "lks"),
prior(normal(log(1.04), 1), nlpar = "lkg"),
prior(normal(0, 0.5), nlpar = "tphi"),
prior(normal(0, 3), lb = 0, nlpar = "lb0", class = "sd"),
prior(normal(0, 3), lb = 0, nlpar = "lks", class = "sd"),
prior(normal(0, 3), lb = 0, nlpar = "lkg", class = "sd"),
prior(student_t(3, 0, 22.2), lb = 0, nlpar = "tphi", class = "sd"),
prior(normal(0, 3), lb = 0, nlpar = "tau")
)
# Initial values to avoid problems at the beginning
n_patients <- nlevels(df$id)
inits <- list(
b_lb0 = array(3.61),
b_lks = array(-1.25),
b_lkg = array(-1.33),
b_tphi = array(0),
sd_1 = array(0.58),
sd_2 = array(1.6),
sd_3 = array(0.994),
sd_4 = array(0.1),
b_tau = array(0.161),
z_1 = matrix(0, nrow = 1, ncol = n_patients),
z_2 = matrix(0, nrow = 1, ncol = n_patients),
z_3 = matrix(0, nrow = 1, ncol = n_patients),
z_4 = matrix(0, nrow = 1, ncol = n_patients)
)
# Fit the model
save_file <- here("session-tgi/gsf1.RData")
if (file.exists(save_file)) {
load(save_file)
} else {
fit <- brm(
formula = formula,
data = df,
prior = priors,
family = gaussian(),
init = rep(list(inits), CHAINS),
chains = CHAINS,
iter = WARMUP + ITER,
warmup = WARMUP,
seed = BAYES.SEED,
refresh = REFRESH
)
save(fit, file = save_file)
}
# Summarize the fit
summary(fit)
```
In total this took 76 minutes on my laptop.
## Parameter estimates
```{r}
#| label: gsf_post_processing
post_df <- as_draws_df(fit)
head(names(post_df), 10)
post_df <- post_df |>
mutate(
theta_b0 = exp(b_lb0_Intercept + sd_id__lb0_Intercept^2 / 2),
theta_ks = exp(b_lks_Intercept + sd_id__lks_Intercept^2 / 2),
theta_kg = exp(b_lkg_Intercept + sd_id__lkg_Intercept^2 / 2),
theta_phi = plogis(b_tphi_Intercept),
omega_0 = sd_id__lb0_Intercept,
omega_s = sd_id__lks_Intercept,
omega_g = sd_id__lkg_Intercept,
omega_phi = sd_id__tphi_Intercept,
cv_0 = sqrt(exp(sd_id__lb0_Intercept^2) - 1),
cv_s = sqrt(exp(sd_id__lks_Intercept^2) - 1),
cv_g = sqrt(exp(sd_id__lkg_Intercept^2) - 1),
sigma = b_tau_Intercept
)
```
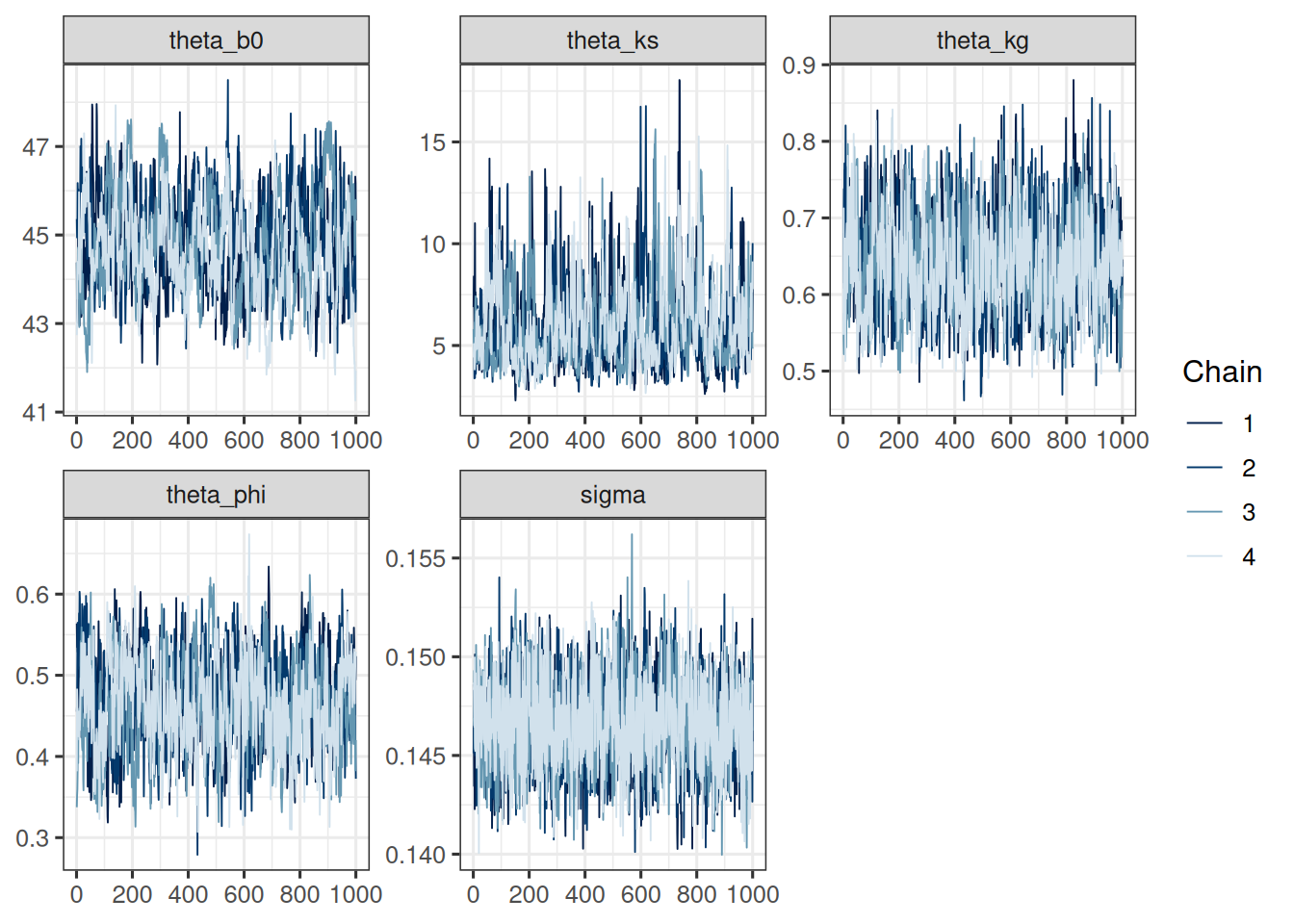
Let's first look at the population level parameters:
```{r}
#| label: gsf_pop_params
gsf_pop_params <- c("theta_b0", "theta_ks", "theta_kg", "theta_phi", "sigma")
mcmc_trace(post_df, pars = gsf_pop_params)
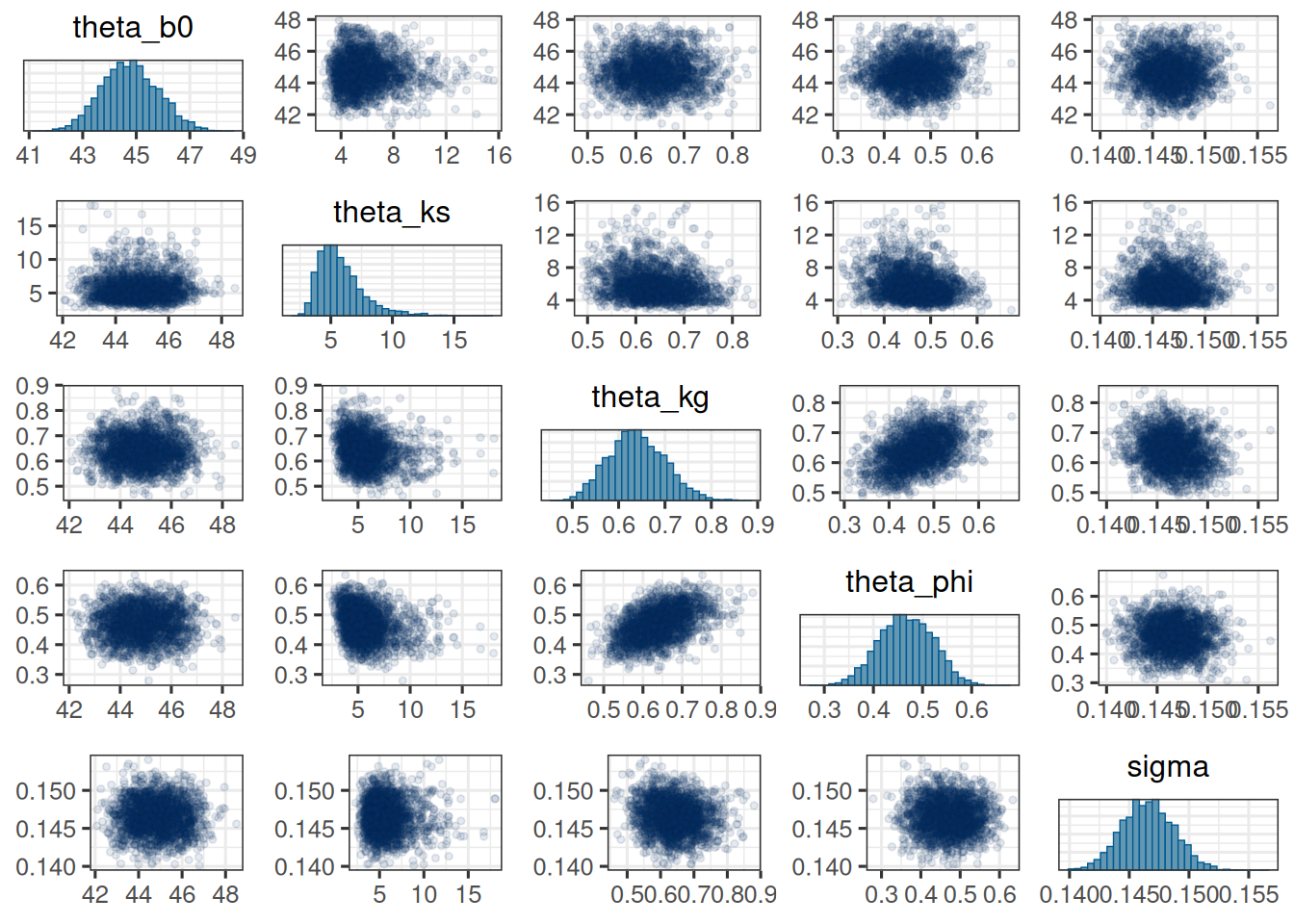
mcmc_pairs(
post_df,
pars = gsf_pop_params,
off_diag_args = list(size = 1, alpha = 0.1)
)
```
The trace plots look good. The chains seem to have converged and the pairs plot shows no strong correlations between the parameters. Let's check the table:
```{r}
#| label: gsf_post_summary
post_sum <- post_df |>
select(theta_b0, theta_ks, theta_kg, theta_phi, omega_0, omega_s, omega_g, omega_phi, sigma) |>
summarize_draws() |>
gt() |>
fmt_number(decimals = 3)
post_sum
```
So $\theta_{\phi}$ is estimated around 0.5. The other parameters are similar to the previous Stein-Fojo model, but we see a larger $\theta_{k_s}$ e.g.
## Observation vs model fit
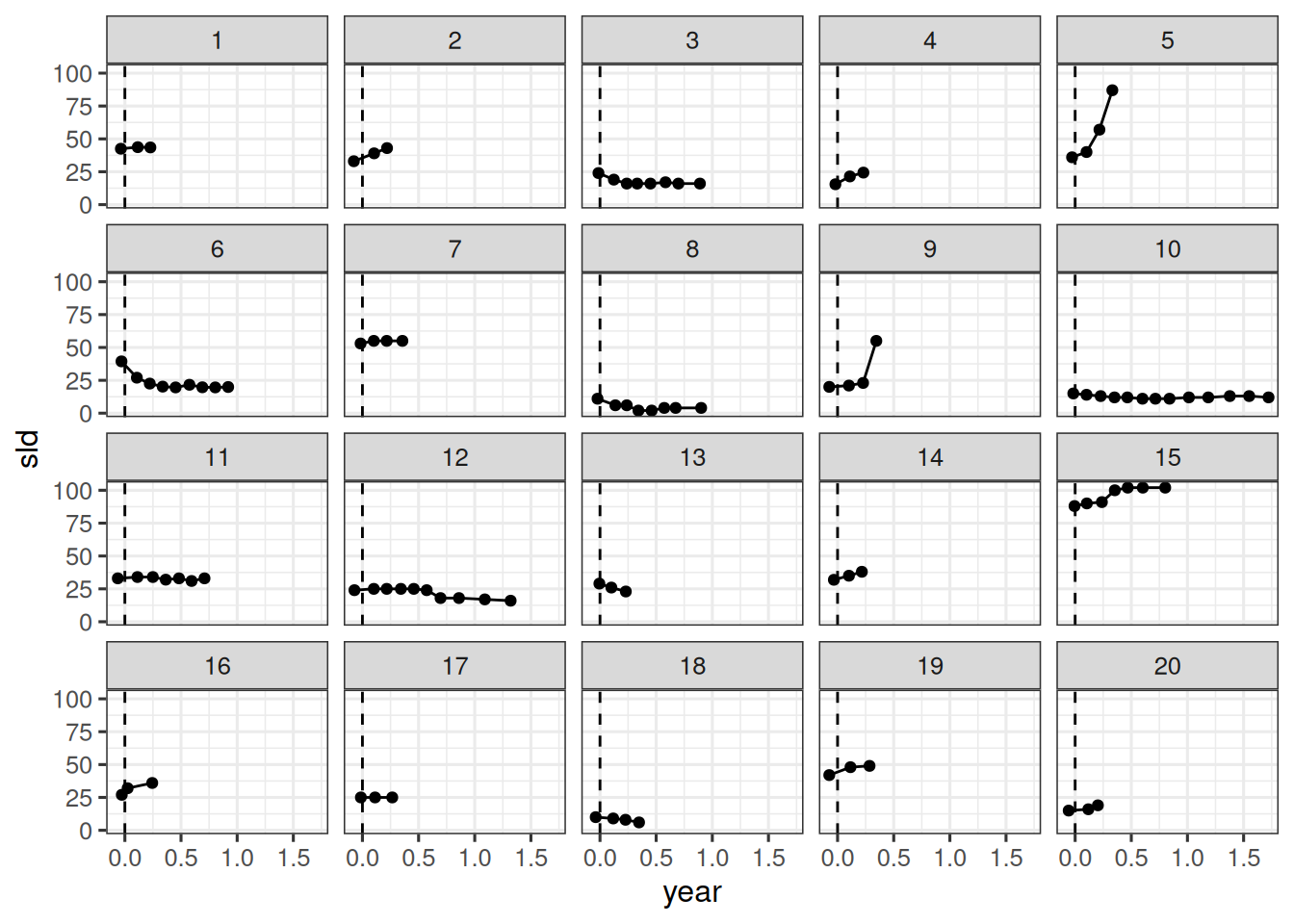
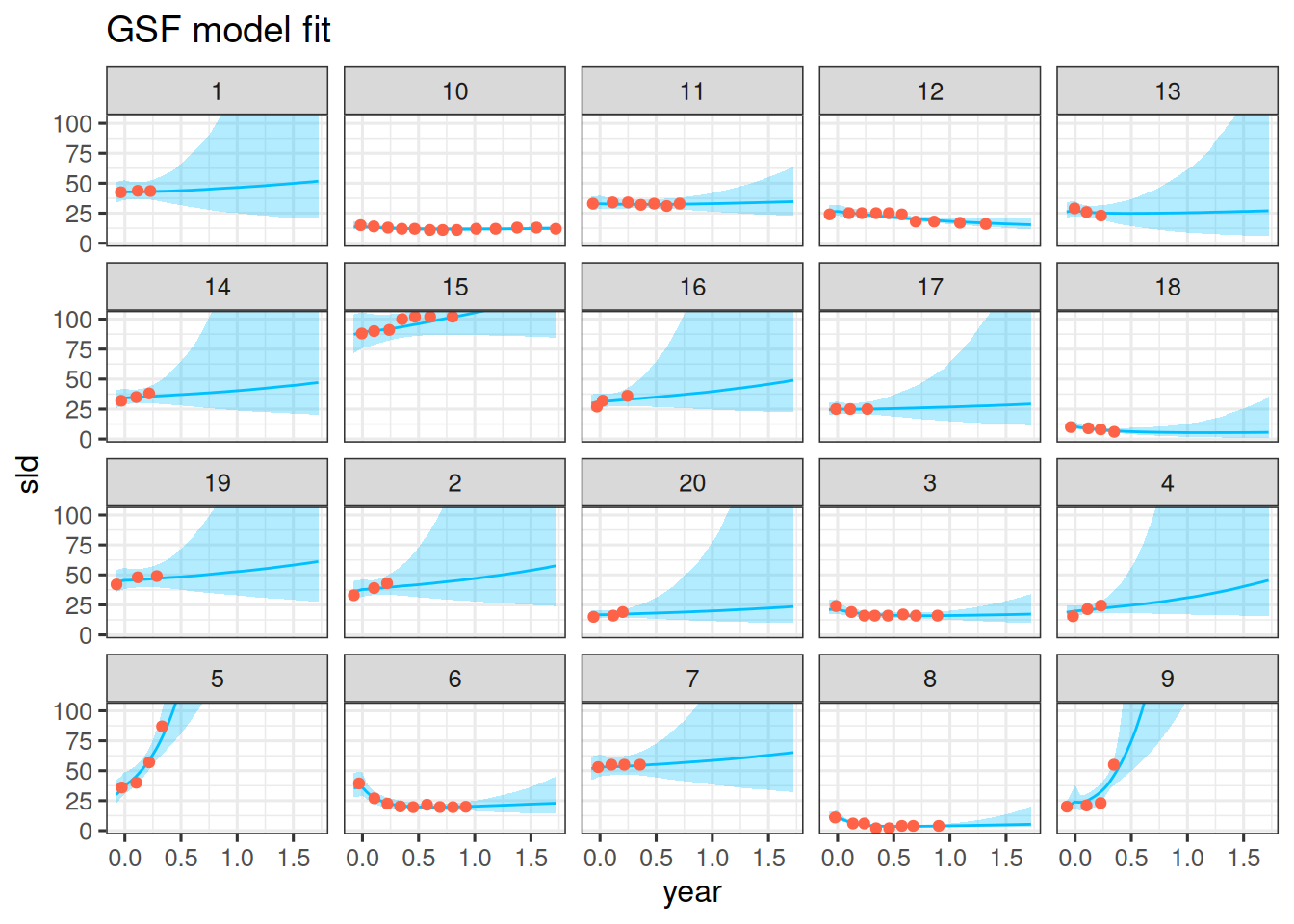
We can now compare the model fit to the observations. Let's do this for the first 20 patients again:
```{r}
#| label: gsf_model_fit
pt_subset <- as.character(1:20)
df_subset <- df |>
filter(id %in% pt_subset)
df_sim <- df_subset |>
data_grid(
id = pt_subset,
year = seq_range(year, 101)
) |>
add_epred_draws(fit) |>
median_qi()
df_sim |>
ggplot(aes(x = year, y = sld)) +
facet_wrap(~ id) +
geom_ribbon(
aes(y = .epred, ymin = .lower, ymax = .upper),
alpha = 0.3,
fill = "deepskyblue"
) +
geom_line(aes(y = .epred), color = "deepskyblue") +
geom_point(data = df_subset, color = "tomato") +
coord_cartesian(ylim = range(df_subset$sld)) +
scale_fill_brewer(palette = "Greys") +
labs(title = "GSF model fit")
```
This also looks good. The model seems to capture the data well.
## With `jmpost`
This model can also be fit with the `jmpost` package. The corresponding function is `LongitudinalGSF`. The statistical model is specified in the vignette [here](https://genentech.github.io/jmpost/main/articles/statistical-specification.html#generalized-stein-fojo-gsf-model).
Homework: Implement the generalized Stein-Fojo model with `jmpost` and compare the results with the `brms` implementation.